plsRcox, Cox-Models in a High Dimensional Setting in R
Frédéric Bertrand and Myriam Maumy-Bertrand
The goal of plsRcox is provide Cox models in a high dimensional setting in R.
plsRcox implements partial least squares Regression and various regular, sparse or kernel, techniques for fitting Cox models in high dimensional settings https://doi.org/10.1093/bioinformatics/btu660, Bastien, P., Bertrand, F., Meyer N., Maumy-Bertrand, M. (2015), Deviance residuals-based sparse PLS and sparse kernel PLS regression for censored data, Bioinformatics, 31(3):397-404. Cross validation criteria were studied in <arXiv:1810.02962>, Bertrand, F., Bastien, Ph. and Maumy-Bertrand, M. (2018), Cross validating extensions of kernel, sparse or regular partial least squares regression models to censored data.
The package was presented at the User2014! conference. Frédéric Bertrand, Philippe Bastien, Nicolas Meyer and Myriam Bertrand (2014). “plsRcox, Cox-Models in a high dimensional setting in R”, book of abstracts, User2014!, Los Angeles, page 177, http://user2014.r-project.org/abstracts/posters/177_Bertrand.pdf.
The plsRcox package contains an original allelotyping dataset from “Allelotyping identification of genomic alterations in rectal chromosomally unstable tumors without preoperative treatment”, Benoît Romain, Agnès Neuville, Nicolas Meyer, Cécile Brigand, Serge Rohr, Anne Schneider, Marie-Pierre Gaub and Dominique Guenot (2010), BMC Cancer, 10:561, https://doi.org/10.1186/1471-2407-10-561.
Support for parallel computation and GPU is being developped.
The package provides several modelling techniques related to penalized Cox models or extensions of partial least squares to Cox models. The first two were new algorithms.
coxsplsDR and cv.coxsplsDR (Philippe Bastien, Frederic Bertrand, Nicolas Meyer, and Myriam Maumy-Bertrand (2015), “Deviance residuals-based sparse PLS and sparse kernel PLS regression for censored data”, Bioinformatics, 31(3):397-404, https://doi.org/10.1093/bioinformatics/btu660),
coxDKsplsDR and cv.coxDKsplsDR (Philippe Bastien, Frederic Bertrand, Nicolas Meyer, and Myriam Maumy-Bertrand (2015), “Deviance residuals-based sparse PLS and sparse kernel PLS regression for censored data”, Bioinformatics, 31(3):397-404, https://doi.org/10.1093/bioinformatics/btu660),
coxDKplsDR and cv.coxDKplsDR (Philippe Bastien (2008), “Deviance residuals based PLS regression for censored data in high dimensional setting”, Chemometrics and Intelligent Laboratory Systems, 91:78–86, https://doi.org/10.1016/j.chemolab.2007.09.009),
coxpls and cv.coxpls (Nguyen, D.V., Rocke, D.M. (2002), “Partial least squares proportional hazard regression for application to DNA microarray survival data”, Bioinformatics, 18(12):1625–1632),
coxplsDR and cv.coxplsDR (Philippe Bastien (2008), “Deviance residuals based PLS regression for censored data in high dimensional setting”, Chemometrics and Intelligent Laboratory Systems, 91:78–86, https://doi.org/10.1016/j.chemolab.2007.09.009),
DKplsRcox,
larsDR and cv.larsDR (Segal, M.R. (2006), “Microarray Gene Expression Data with Linked Survival Phenotypes: Diffuse large-B- Cell Lymphoma Revisited”, Biostatistics, 7:268-285, https://doi.org/10.1093/biostatistics/kxj006),
plsRcox and cv.plsRcox (Philippe Bastien, Vincenzo Esposito Vinzi, and Michel Tenenhaus (2005), “PLS generalised linear regression”, Computational Statistics & Data Analysis, 48(1):17–46, https://doi.org/10.1016/j.csda.2004.02.005),
autoplsRcox and cv.autoplsRcox (Philippe Bastien, Vincenzo Esposito Vinzi, and Michel Tenenhaus (2005), “PLS generalised linear regression”, Computational Statistics & Data Analysis, 48(1):17–46, https://doi.org/10.1016/j.csda.2004.02.005),
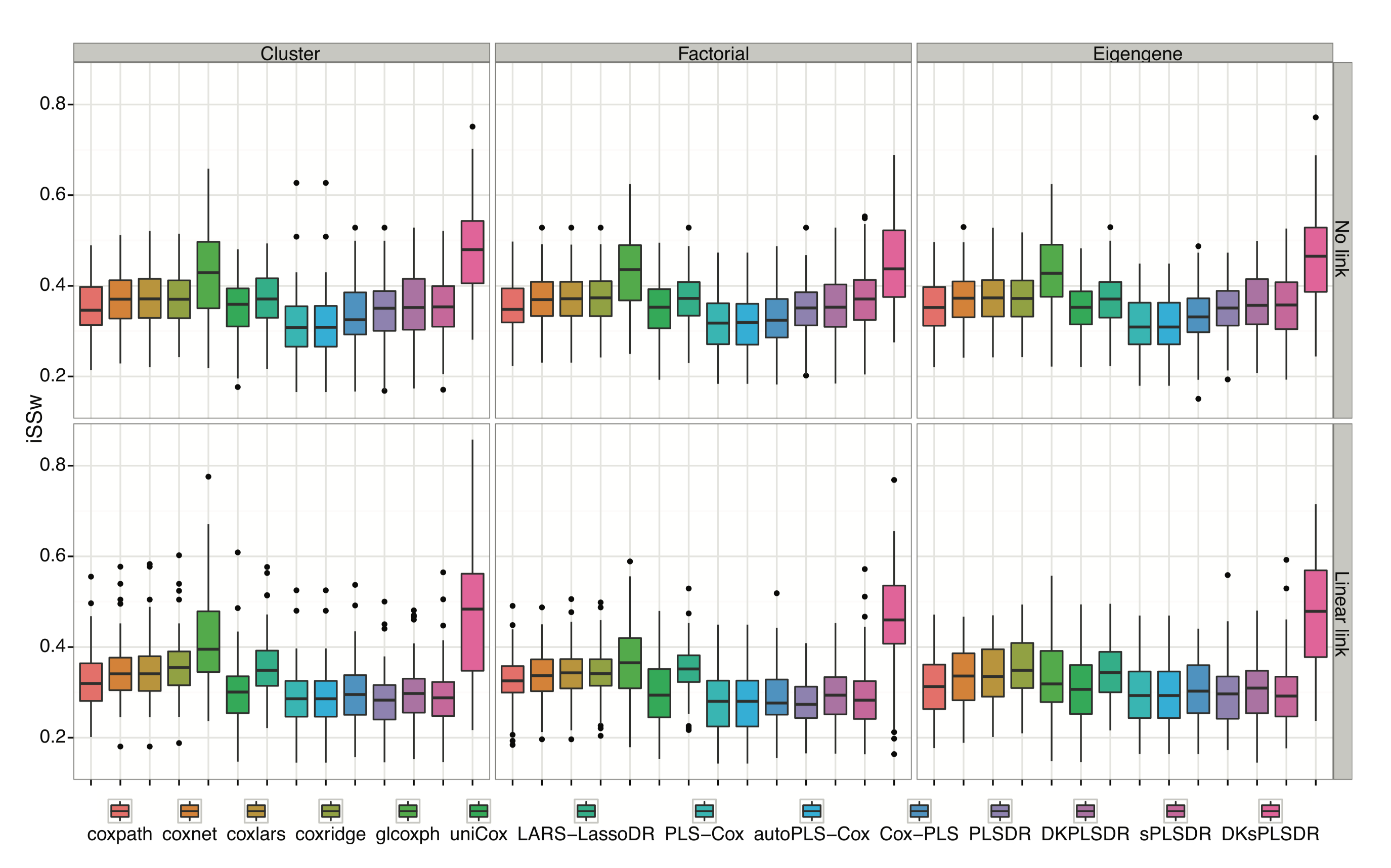
Performance comparisons.
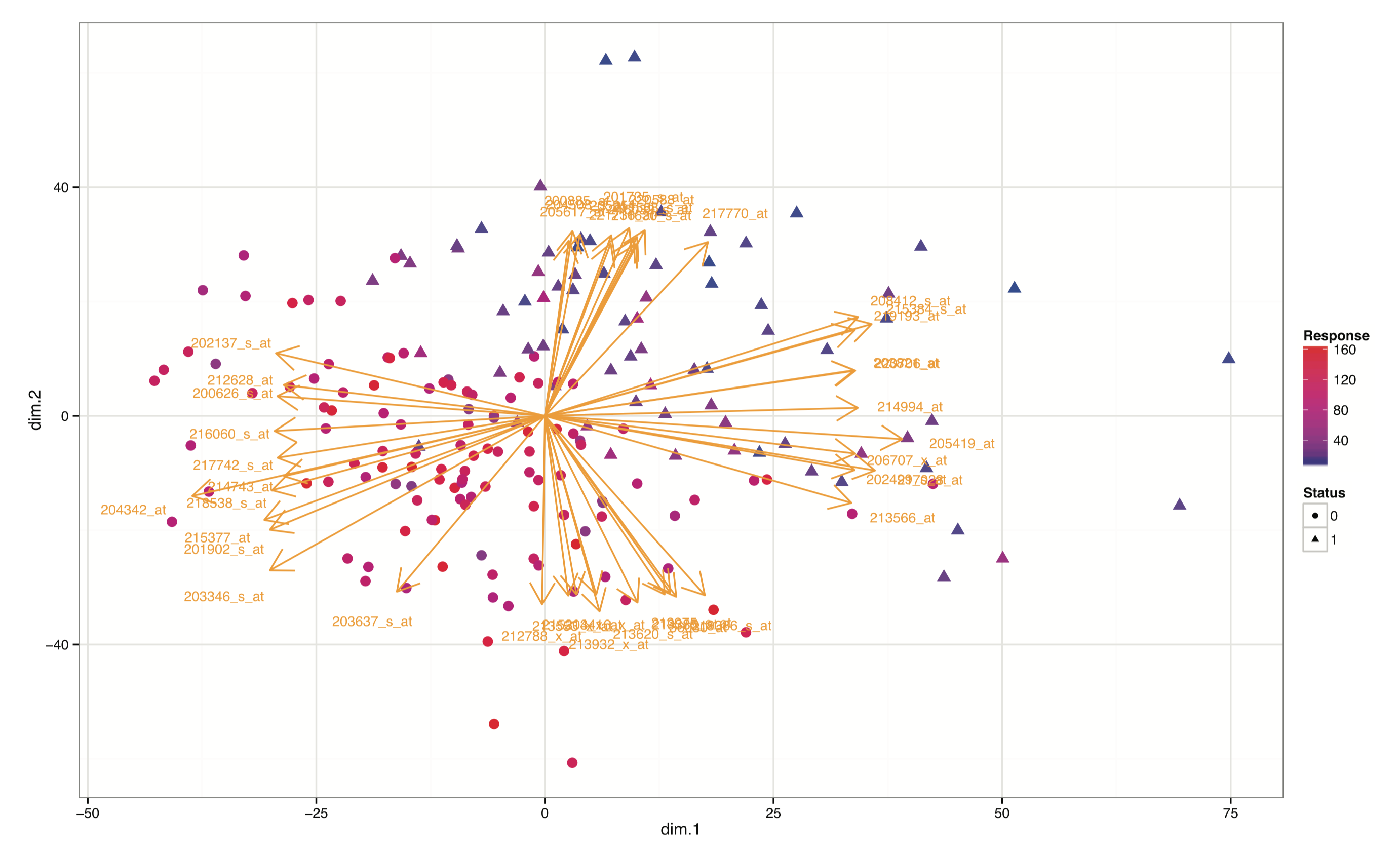
Example of biplot of data.
This website and these examples were created by F. Bertrand and M. Maumy-Bertrand.
Installation
You can install the released version of plsRcox from CRAN with:
install.packages("plsRcox")You can install the development version of plsRcox from github with:
devtools::install_github("fbertran/plsRcox")Example
The original allelotyping dataset
library(plsRcox)
data(micro.censure)
Y_train_micro <- micro.censure$survyear[1:80]
C_train_micro <- micro.censure$DC[1:80]
Y_test_micro <- micro.censure$survyear[81:117]
C_test_micro <- micro.censure$DC[81:117]
data(Xmicro.censure_compl_imp)
X_train_micro <- apply((as.matrix(Xmicro.censure_compl_imp)),FUN="as.numeric",MARGIN=2)[1:80,]
X_train_micro_df <- data.frame(X_train_micro)Compute deviance residuals with some options.
DR_coxph(Y_train_micro,C_train_micro,plot=TRUE)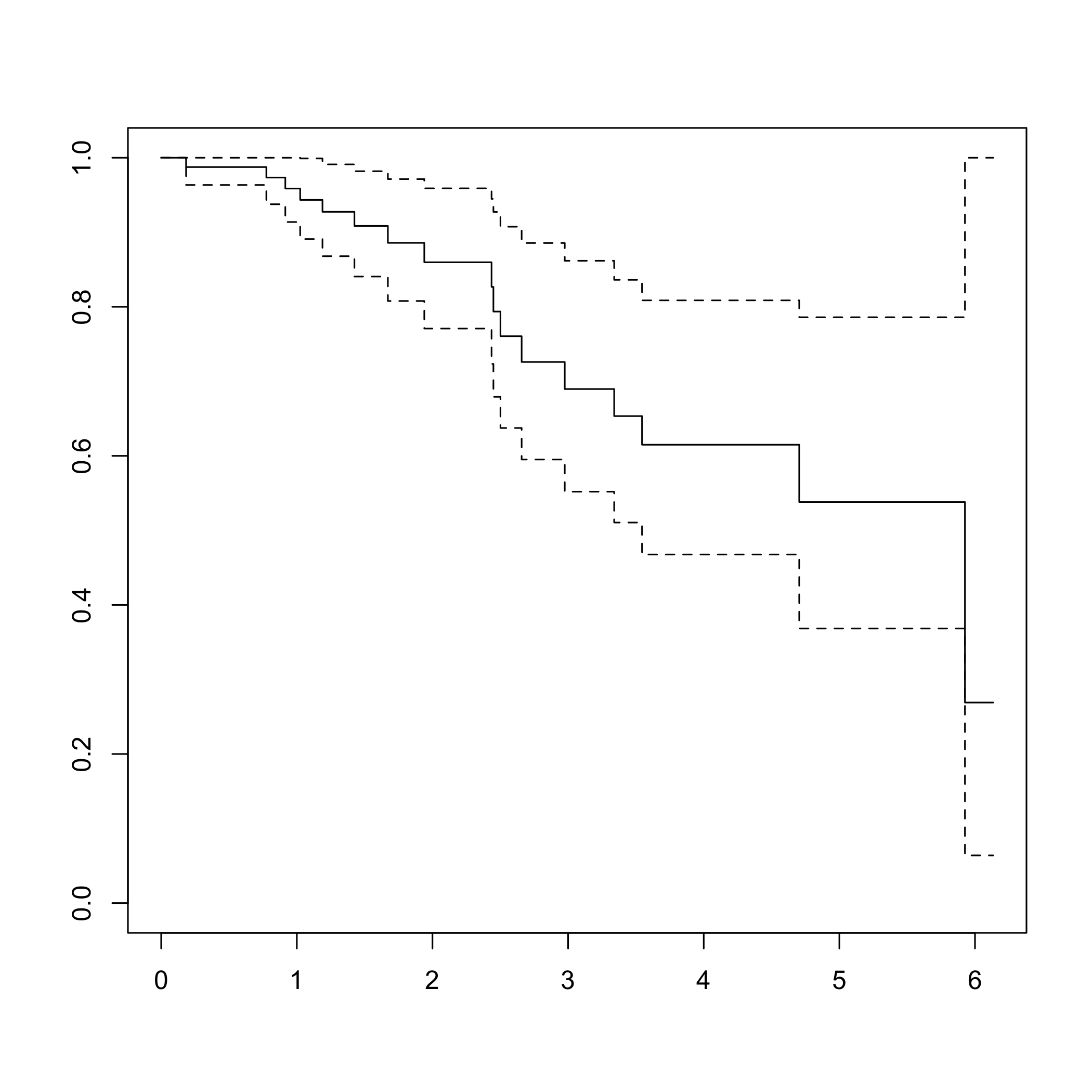
#> 1 2 3 4 5 6
#> -1.48432960 -0.54695398 -0.23145502 -0.34003013 -0.97633722 -0.38667660
#> 7 8 9 10 11 12
#> -0.38667660 1.57418914 -0.54695398 -0.15811388 2.10405254 -0.23145502
#> 13 14 15 16 17 18
#> -0.38667660 -1.09692040 -0.15811388 -0.15811388 -0.54695398 -0.38667660
#> 19 20 21 22 23 24
#> 0.65978609 -1.09692040 -0.43627414 -0.28961087 -0.38667660 -0.97633722
#> 25 26 27 28 29 30
#> -1.09692040 -0.15811388 -0.43627414 -0.43627414 -0.38667660 -0.23145502
#> 31 32 33 34 35 36
#> 2.30072697 -0.49023986 -0.54695398 -0.73444882 1.31082939 -0.97633722
#> 37 38 39 40 41 42
#> 1.70134282 -0.54695398 -0.15811388 1.07714870 -0.15811388 -0.49023986
#> 43 44 45 46 47 48
#> -0.34003013 -0.97633722 -0.15811388 -0.91410465 -1.09692040 -0.43627414
#> 49 50 51 52 53 54
#> -0.38667660 -0.09836581 -0.79392956 0.46851068 -0.34003013 1.95366297
#> 55 56 57 58 59 60
#> 2.60558118 -0.54695398 -1.09692040 -0.15811388 -0.49023986 -0.97633722
#> 61 62 63 64 65 66
#> -0.28961087 1.44879795 1.82660327 -0.38667660 0.96936094 -0.15811388
#> 67 68 69 70 71 72
#> -0.43627414 -0.49023986 1.18850436 -0.97633722 -0.97633722 0.86322194
#> 73 74 75 76 77 78
#> -0.43627414 -0.49023986 -0.38667660 0.76231394 -0.97633722 -0.43627414
#> 79 80
#> -0.54695398 -0.43627414
DR_coxph(Y_train_micro,C_train_micro,scaleY=FALSE,plot=TRUE)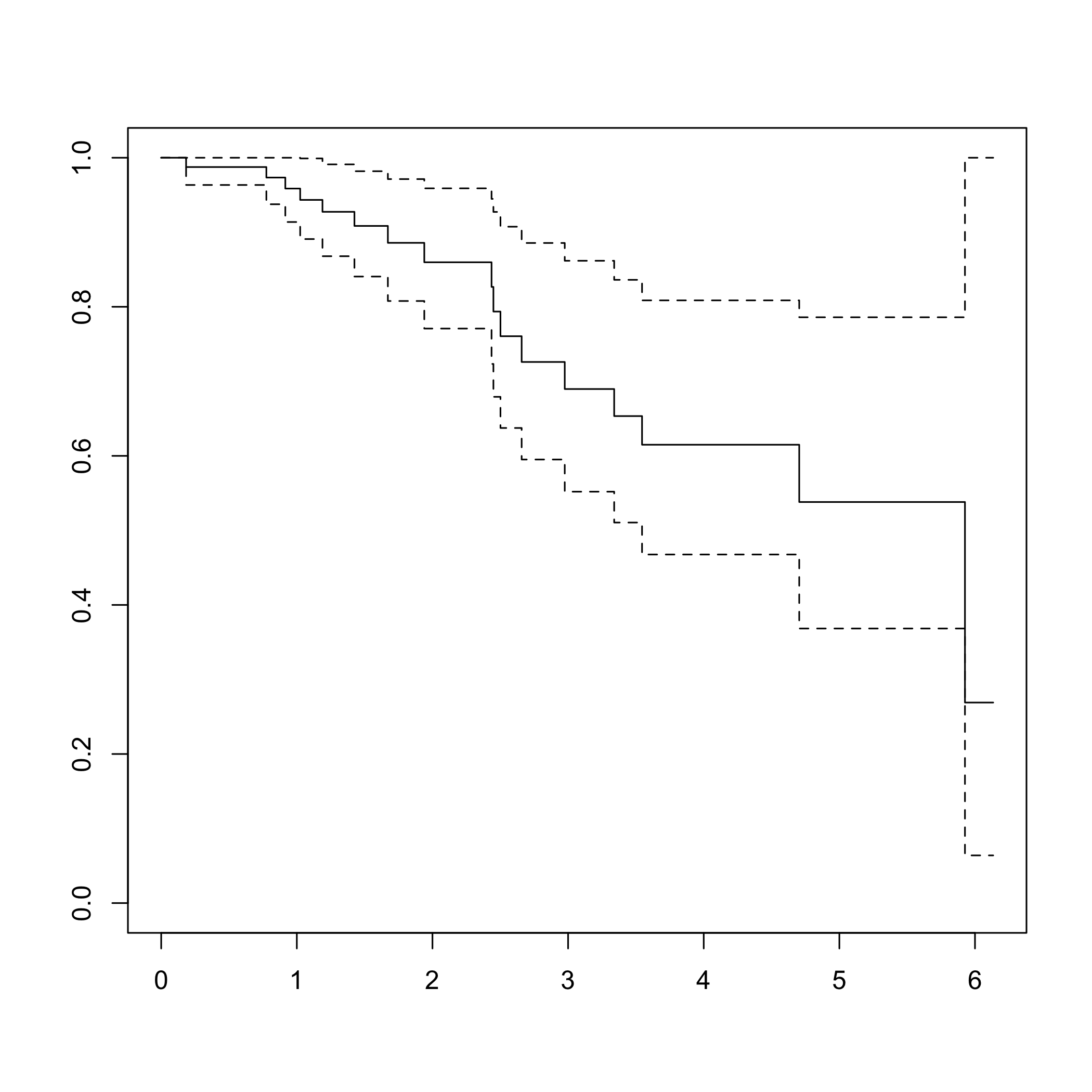
#> 1 2 3 4 5 6
#> -1.48432960 -0.54695398 -0.23145502 -0.34003013 -0.97633722 -0.38667660
#> 7 8 9 10 11 12
#> -0.38667660 1.57418914 -0.54695398 -0.15811388 2.10405254 -0.23145502
#> 13 14 15 16 17 18
#> -0.38667660 -1.09692040 -0.15811388 -0.15811388 -0.54695398 -0.38667660
#> 19 20 21 22 23 24
#> 0.65978609 -1.09692040 -0.43627414 -0.28961087 -0.38667660 -0.97633722
#> 25 26 27 28 29 30
#> -1.09692040 -0.15811388 -0.43627414 -0.43627414 -0.38667660 -0.23145502
#> 31 32 33 34 35 36
#> 2.30072697 -0.49023986 -0.54695398 -0.73444882 1.31082939 -0.97633722
#> 37 38 39 40 41 42
#> 1.70134282 -0.54695398 -0.15811388 1.07714870 -0.15811388 -0.49023986
#> 43 44 45 46 47 48
#> -0.34003013 -0.97633722 -0.15811388 -0.91410465 -1.09692040 -0.43627414
#> 49 50 51 52 53 54
#> -0.38667660 -0.09836581 -0.79392956 0.46851068 -0.34003013 1.95366297
#> 55 56 57 58 59 60
#> 2.60558118 -0.54695398 -1.09692040 -0.15811388 -0.49023986 -0.97633722
#> 61 62 63 64 65 66
#> -0.28961087 1.44879795 1.82660327 -0.38667660 0.96936094 -0.15811388
#> 67 68 69 70 71 72
#> -0.43627414 -0.49023986 1.18850436 -0.97633722 -0.97633722 0.86322194
#> 73 74 75 76 77 78
#> -0.43627414 -0.49023986 -0.38667660 0.76231394 -0.97633722 -0.43627414
#> 79 80
#> -0.54695398 -0.43627414
DR_coxph(Y_train_micro,C_train_micro,scaleY=TRUE,plot=TRUE)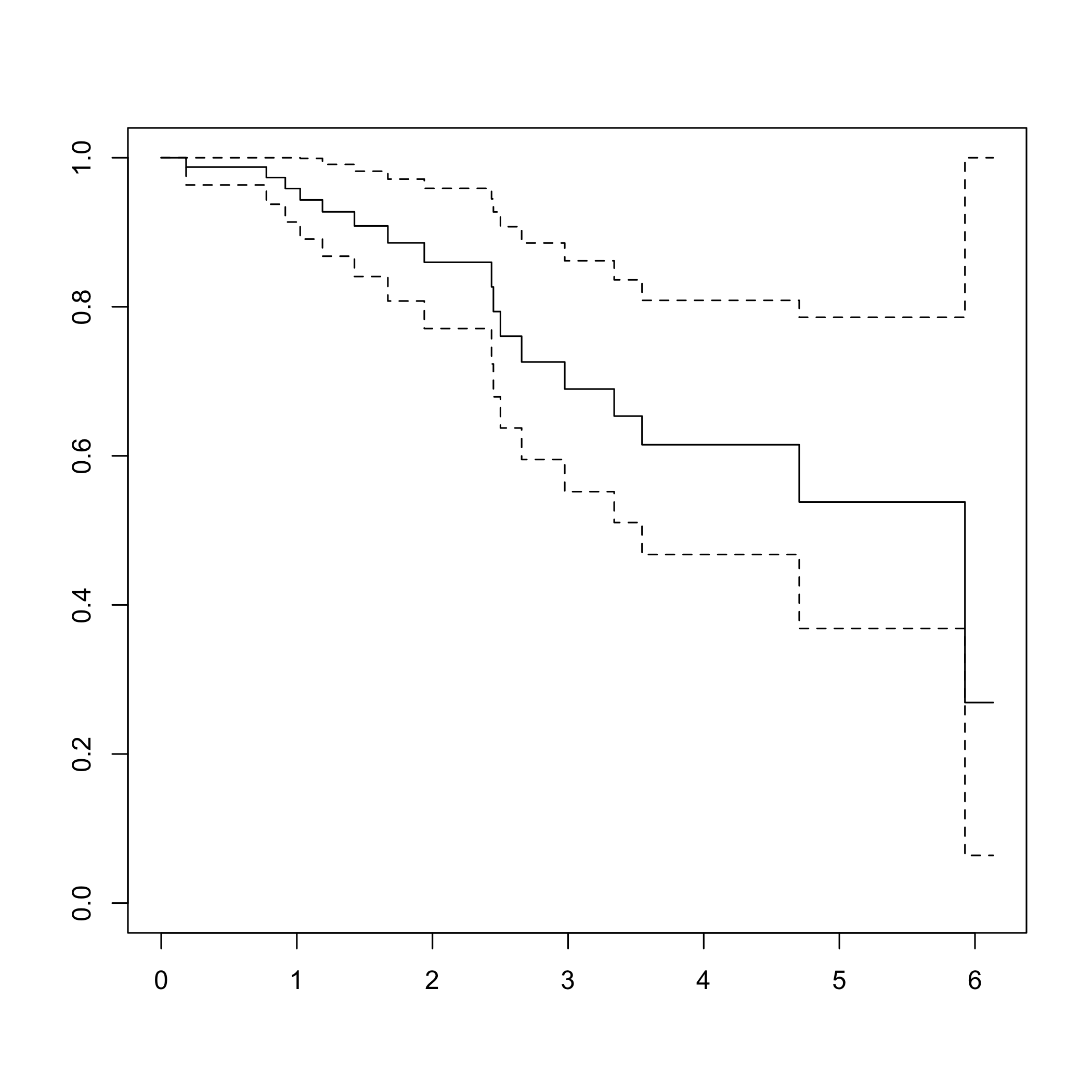
#> 1 2 3 4 5 6
#> -1.48432960 -0.54695398 -0.23145502 -0.34003013 -0.97633722 -0.38667660
#> 7 8 9 10 11 12
#> -0.38667660 1.57418914 -0.54695398 -0.15811388 2.10405254 -0.23145502
#> 13 14 15 16 17 18
#> -0.38667660 -1.09692040 -0.15811388 -0.15811388 -0.54695398 -0.38667660
#> 19 20 21 22 23 24
#> 0.65978609 -1.09692040 -0.43627414 -0.28961087 -0.38667660 -0.97633722
#> 25 26 27 28 29 30
#> -1.09692040 -0.15811388 -0.43627414 -0.43627414 -0.38667660 -0.23145502
#> 31 32 33 34 35 36
#> 2.30072697 -0.49023986 -0.54695398 -0.73444882 1.31082939 -0.97633722
#> 37 38 39 40 41 42
#> 1.70134282 -0.54695398 -0.15811388 1.07714870 -0.15811388 -0.49023986
#> 43 44 45 46 47 48
#> -0.34003013 -0.97633722 -0.15811388 -0.91410465 -1.09692040 -0.43627414
#> 49 50 51 52 53 54
#> -0.38667660 -0.09836581 -0.79392956 0.46851068 -0.34003013 1.95366297
#> 55 56 57 58 59 60
#> 2.60558118 -0.54695398 -1.09692040 -0.15811388 -0.49023986 -0.97633722
#> 61 62 63 64 65 66
#> -0.28961087 1.44879795 1.82660327 -0.38667660 0.96936094 -0.15811388
#> 67 68 69 70 71 72
#> -0.43627414 -0.49023986 1.18850436 -0.97633722 -0.97633722 0.86322194
#> 73 74 75 76 77 78
#> -0.43627414 -0.49023986 -0.38667660 0.76231394 -0.97633722 -0.43627414
#> 79 80
#> -0.54695398 -0.43627414coxsplsDR
(cox_splsDR_fit=coxsplsDR(X_train_micro,Y_train_micro,C_train_micro,ncomp=6,eta=.5))
#> Call:
#> coxph(formula = YCsurv ~ ., data = tt_splsDR)
#>
#> coef exp(coef) se(coef) z p
#> dim.1 0.8093 2.2462 0.2029 3.989 6.63e-05
#> dim.2 0.9295 2.5333 0.2939 3.163 0.00156
#> dim.3 0.9968 2.7096 0.4190 2.379 0.01736
#> dim.4 0.9705 2.6391 0.3793 2.558 0.01052
#> dim.5 0.2162 1.2413 0.2811 0.769 0.44192
#> dim.6 0.4380 1.5496 0.3608 1.214 0.22473
#>
#> Likelihood ratio test=55.06 on 6 df, p=4.51e-10
#> n= 80, number of events= 17
(cox_splsDR_fit2=coxsplsDR(~X_train_micro,Y_train_micro,C_train_micro,ncomp=6,eta=.5,trace=TRUE))
#> Error in model.matrix(mt0, mf0, , contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
(cox_splsDR_fit3=coxsplsDR(~.,Y_train_micro,C_train_micro,ncomp=6,
dataXplan=X_train_micro_df,eta=.5))
#> Error in model.matrix(mt0, mf0, , contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
rm(cox_splsDR_fit,cox_splsDR_fit2,cox_splsDR_fit3)
#> Warning in rm(cox_splsDR_fit, cox_splsDR_fit2, cox_splsDR_fit3): objet
#> 'cox_splsDR_fit2' introuvable
#> Warning in rm(cox_splsDR_fit, cox_splsDR_fit2, cox_splsDR_fit3): objet
#> 'cox_splsDR_fit3' introuvablecv.coxsplsDR
set.seed(123456)
(cv.coxsplsDR.res=cv.coxsplsDR(list(x=X_train_micro,time=Y_train_micro, status=C_train_micro),nt=10,eta=.1))
#> CV Fold 1
#> CV Fold 2
#> CV Fold 3
#> CV Fold 4
#> CV Fold 5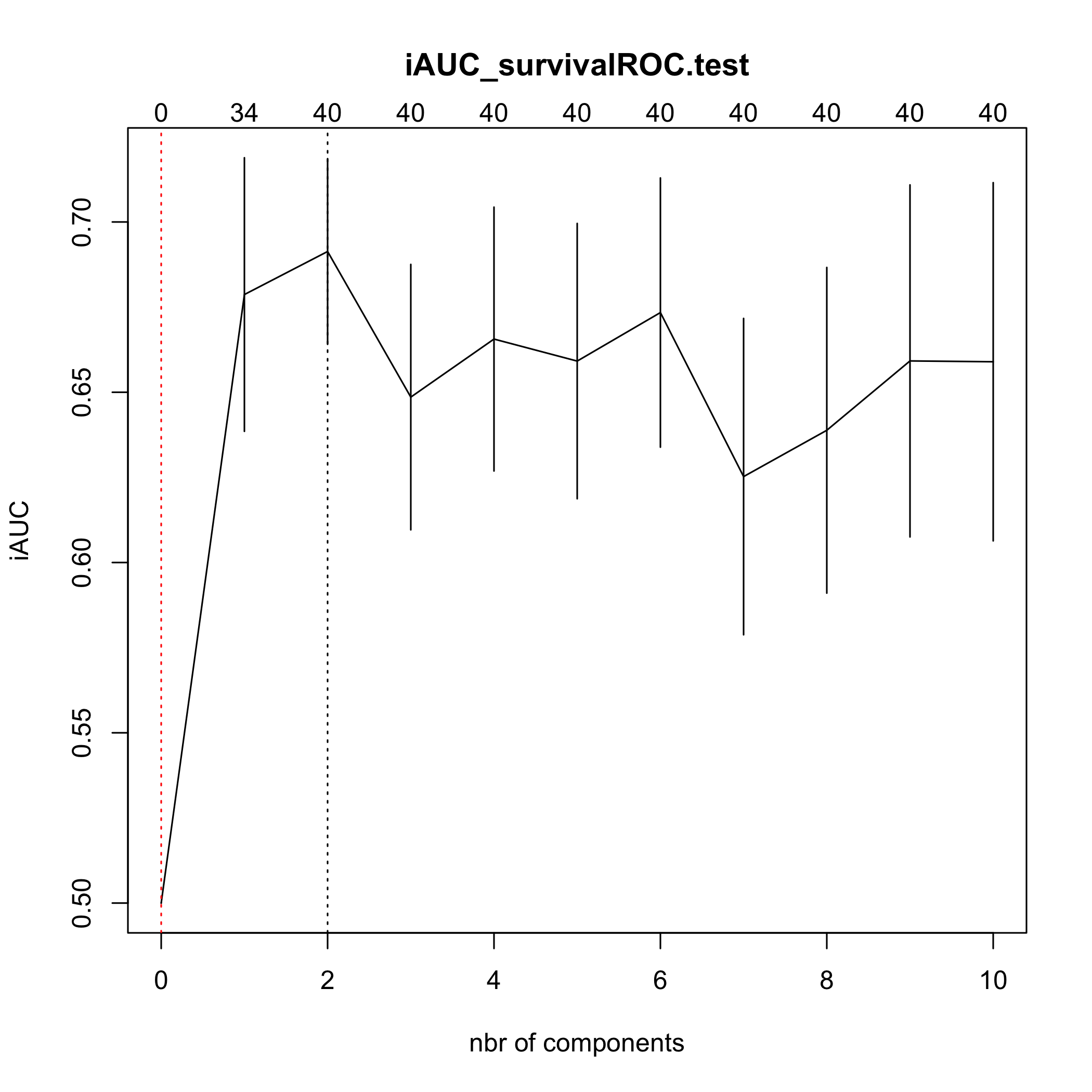
#> $nt
#> [1] 10
#>
#> $cv.error10
#> [1] 0.5000000 0.6786893 0.6913293 0.6485690 0.6656184 0.6591497 0.6733976
#> [8] 0.6252317 0.6388320 0.6592004 0.6589521
#>
#> $cv.se10
#> [1] 0.00000000 0.04017423 0.02726346 0.03897730 0.03874068 0.04042522 0.03952962
#> [8] 0.04645295 0.04782038 0.05168926 0.05259748
#>
#> $folds
#> $folds$`1`
#> [1] 60 3 2 14 77 6 50 4 72 32 22 1 41 21 63 25
#>
#> $folds$`2`
#> [1] 42 67 65 15 73 48 57 26 7 13 31 53 5 27 37 64
#>
#> $folds$`3`
#> [1] 71 23 56 35 75 29 30 18 62 44 12 33 68 49 43 55
#>
#> $folds$`4`
#> [1] 54 76 24 16 34 66 9 11 69 40 70 36 39 8 19 20
#>
#> $folds$`5`
#> [1] 74 38 46 80 47 78 10 45 51 28 61 79 58 17 52 59
#>
#>
#> $lambda.min10
#> [1] 2
#>
#> $lambda.1se10
#> [1] 0
#>
#> $nzb
#> [1] 0 34 40 40 40 40 40 40 40 40 40coxDKsplsDR
(cox_DKsplsDR_fit=coxDKsplsDR(X_train_micro,Y_train_micro,C_train_micro,ncomp=6, validation="CV",eta=.5))
#> Kernel : rbfdot
#> Estimated_sigma 0.0122308
#> Call:
#> coxph(formula = YCsurv ~ ., data = tt_DKsplsDR)
#>
#> coef exp(coef) se(coef) z p
#> dim.1 3.633e+00 3.783e+01 1.245e+00 2.918 0.00352
#> dim.2 9.905e+00 2.003e+04 3.297e+00 3.004 0.00266
#> dim.3 6.491e+00 6.589e+02 2.575e+00 2.521 0.01170
#> dim.4 1.465e+01 2.308e+06 4.848e+00 3.022 0.00251
#> dim.5 6.103e+00 4.473e+02 2.757e+00 2.213 0.02687
#> dim.6 1.249e+01 2.664e+05 4.980e+00 2.508 0.01212
#>
#> Likelihood ratio test=69.55 on 6 df, p=5.067e-13
#> n= 80, number of events= 17
(cox_DKsplsDR_fit=coxDKsplsDR(~X_train_micro,Y_train_micro,C_train_micro,ncomp=6, validation="CV",eta=.5))
#> Error in model.matrix(mt0, mf0, , contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
(cox_DKsplsDR_fit=coxDKsplsDR(~.,Y_train_micro,C_train_micro,ncomp=6,
validation="CV",dataXplan=data.frame(X_train_micro),eta=.5))
#> Error in model.matrix(mt0, mf0, , contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
rm(cox_DKsplsDR_fit)cv.coxsplsDR
set.seed(123456)
(cv.coxDKsplsDR.res=cv.coxDKsplsDR(list(x=X_train_micro,time=Y_train_micro, status=C_train_micro),nt=10,eta=.1))
#> Kernel : rbfdot
#> Estimated_sigma 0.01257168
#> CV Fold 1
#> Kernel : rbfdot
#> Estimated_sigma 0.01198263
#> CV Fold 2
#> Kernel : rbfdot
#> Estimated_sigma 0.01156809
#> CV Fold 3
#> Kernel : rbfdot
#> Estimated_sigma 0.01287851
#> CV Fold 4
#> Kernel : rbfdot
#> Estimated_sigma 0.01127231
#> CV Fold 5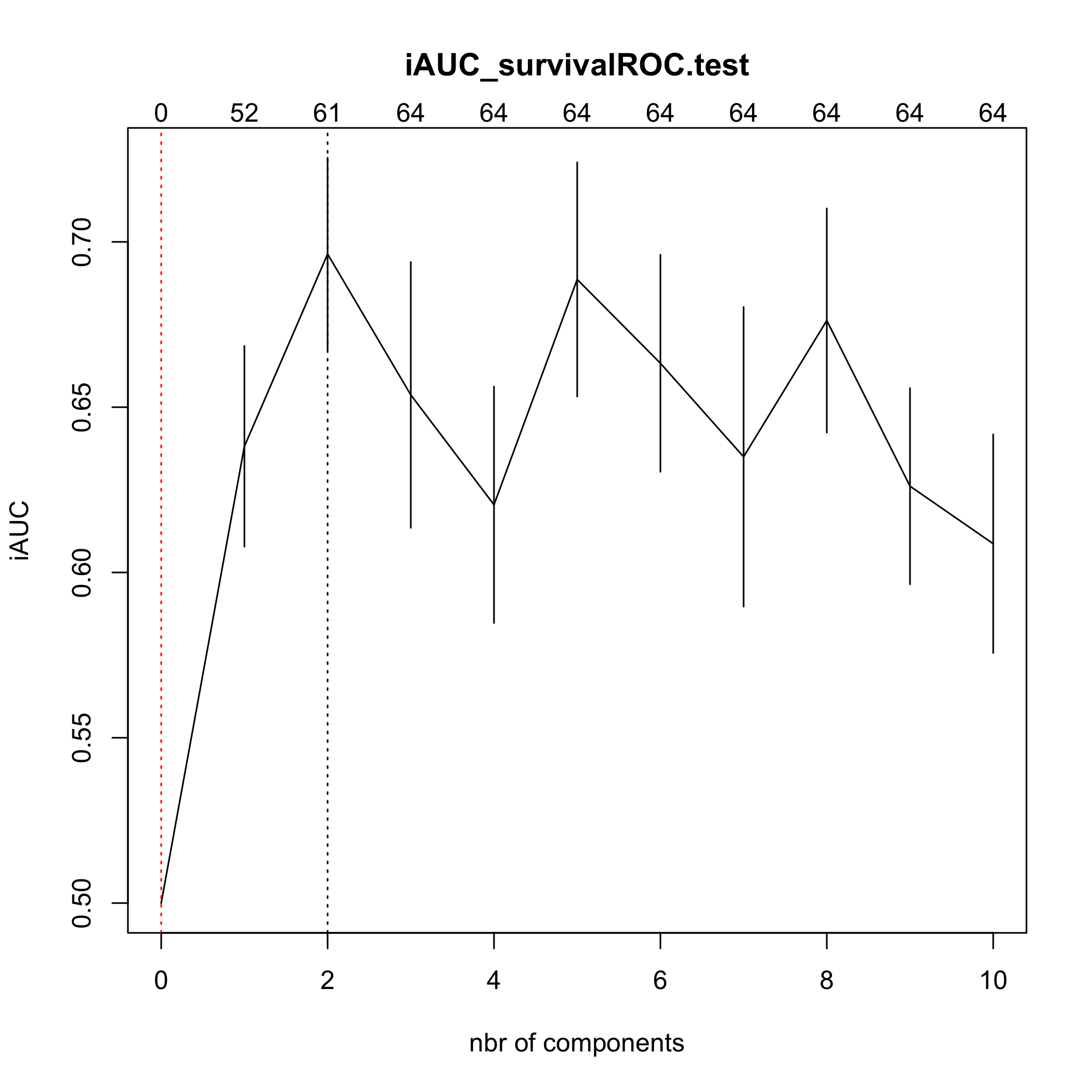
#> $nt
#> [1] 10
#>
#> $cv.error10
#> [1] 0.5000000 0.6381540 0.6963262 0.6537039 0.6204813 0.6886401 0.6632860
#> [8] 0.6349883 0.6762113 0.6261072 0.6087014
#>
#> $cv.se10
#> [1] 0.00000000 0.03036225 0.02912723 0.04020941 0.03577022 0.03542745 0.03283778
#> [8] 0.04532447 0.03390654 0.02968504 0.03306444
#>
#> $folds
#> $folds$`1`
#> [1] 60 3 2 14 77 6 50 4 72 32 22 1 41 21 63 25
#>
#> $folds$`2`
#> [1] 42 67 65 15 73 48 57 26 7 13 31 53 5 27 37 64
#>
#> $folds$`3`
#> [1] 71 23 56 35 75 29 30 18 62 44 12 33 68 49 43 55
#>
#> $folds$`4`
#> [1] 54 76 24 16 34 66 9 11 69 40 70 36 39 8 19 20
#>
#> $folds$`5`
#> [1] 74 38 46 80 47 78 10 45 51 28 61 79 58 17 52 59
#>
#>
#> $lambda.min10
#> [1] 2
#>
#> $lambda.1se10
#> [1] 0
#>
#> $nzb
#> [1] 0 52 61 64 64 64 64 64 64 64 64plsRcox
plsRcox(X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5)
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Component____ 4 ____
#> ____Component____ 5 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> Number of required components:
#> [1] 5
#> Number of successfully computed components:
#> [1] 5
#> Coefficients:
#> [,1]
#> D18S61 0.68964919
#> D17S794 -1.14362392
#> D13S173 1.37632457
#> D20S107 4.96128745
#> TP53 1.68453950
#> D9S171 -1.46691252
#> D8S264 0.66710776
#> D5S346 -4.61338196
#> D22S928 -1.82005524
#> D18S53 0.79853646
#> D1S225 -1.46234986
#> D3S1282 -1.67925042
#> D15S127 3.92225537
#> D1S305 -2.29680161
#> D1S207 2.02539691
#> D2S138 -3.48975878
#> D16S422 -2.92189625
#> D9S179 -0.59484679
#> D10S191 -1.30136747
#> D4S394 1.34265359
#> D1S197 -0.75014044
#> D6S264 1.32746604
#> D14S65 -3.20882866
#> D17S790 0.55427680
#> D5S430 3.40654627
#> D3S1283 2.12510239
#> D4S414 2.73619967
#> D8S283 0.71955323
#> D11S916 1.45026508
#> D2S159 0.90293134
#> D16S408 -0.59719901
#> D6S275 -1.02204186
#> D10S192 1.14220367
#> sexe 0.67314561
#> Agediag 0.04908478
#> Siege -0.41985924
#> T 2.70581463
#> N 2.47039973
#> M -4.53213922
#> STADE 0.48221697
#> Information criteria and Fit statistics:
#> AIC BIC
#> Nb_Comp_0 112.87990 112.87990
#> Nb_Comp_1 85.11075 87.49278
#> Nb_Comp_2 75.49537 80.25942
#> Nb_Comp_3 68.45852 75.60460
#> Nb_Comp_4 63.09284 72.62094
#> Nb_Comp_5 55.30567 67.21581
plsRcox(~X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5)
#> Error in model.matrix(mt0, mf0, contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
plsRcox(Xplan=X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5,sparse=TRUE, alpha.pvals.expli=.15)
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> Warning : 25 < 10^{-12}
#> Warning only 3 components could thus be extracted
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> Number of required components:
#> [1] 5
#> Number of successfully computed components:
#> [1] 3
#> Coefficients:
#> [,1]
#> D18S61 0.00000000
#> D17S794 0.00000000
#> D13S173 0.00000000
#> D20S107 2.22871454
#> TP53 0.00000000
#> D9S171 0.00000000
#> D8S264 0.00000000
#> D5S346 -1.20298526
#> D22S928 0.00000000
#> D18S53 0.00000000
#> D1S225 -1.29459798
#> D3S1282 -1.99426291
#> D15S127 1.39645601
#> D1S305 0.00000000
#> D1S207 1.25164327
#> D2S138 -1.65740160
#> D16S422 0.00000000
#> D9S179 0.00000000
#> D10S191 -1.25360805
#> D4S394 0.00000000
#> D1S197 0.00000000
#> D6S264 0.00000000
#> D14S65 -1.33587373
#> D17S790 0.00000000
#> D5S430 1.72799213
#> D3S1283 0.00000000
#> D4S414 1.03558702
#> D8S283 0.00000000
#> D11S916 0.00000000
#> D2S159 0.00000000
#> D16S408 -1.75748257
#> D6S275 0.00000000
#> D10S192 0.00000000
#> sexe 0.00000000
#> Agediag 0.05075304
#> Siege 0.00000000
#> T 1.36569407
#> N 1.27485618
#> M -1.17682617
#> STADE -0.65106093
#> Information criteria and Fit statistics:
#> AIC BIC
#> Nb_Comp_0 112.87990 112.87990
#> Nb_Comp_1 85.54313 87.92516
#> Nb_Comp_2 75.16125 79.92530
#> Nb_Comp_3 73.63097 80.77705
plsRcox(Xplan=~X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5,sparse=TRUE, alpha.pvals.expli=.15)
#> Error in model.matrix(mt0, mf0, contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défautcv.plsRcox
set.seed(123456)
(cv.plsRcox.res=cv.plsRcox(list(x=X_train_micro,time=Y_train_micro,status=C_train_micro),nt=10,verbose = FALSE))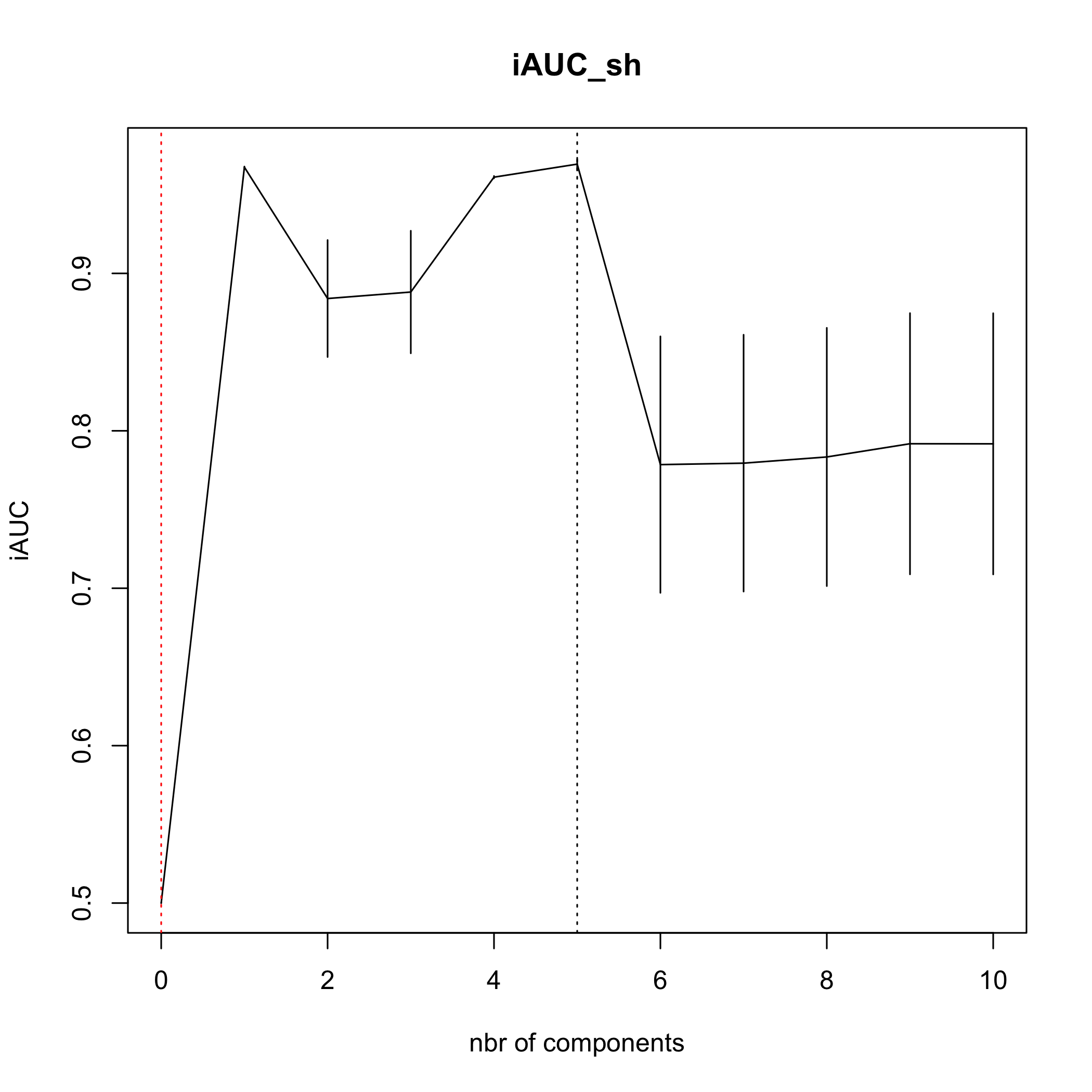
#> $nt
#> [1] 10
#>
#> $cv.error5
#> [1] 0.5000000 0.9674493 0.8840340 0.8881565 0.9611293 0.9694122 0.7785264
#> [8] 0.7794468 0.7833874 0.7917907 0.7917344
#>
#> $cv.se5
#> [1] 0.0000000000 0.0004328242 0.0371488864 0.0389160733 0.0007452107
#> [6] 0.0040593349 0.0814540651 0.0815717378 0.0820171451 0.0829659086
#> [11] 0.0829564223
#>
#> $folds
#> $folds$`1`
#> [1] 60 3 2 14 77 6 50 4 72 32 22 1 41 21 63 25
#>
#> $folds$`2`
#> [1] 42 67 65 15 73 48 57 26 7 13 31 53 5 27 37 64
#>
#> $folds$`3`
#> [1] 71 23 56 35 75 29 30 18 62 44 12 33 68 49 43 55
#>
#> $folds$`4`
#> [1] 54 76 24 16 34 66 9 11 69 40 70 36 39 8 19 20
#>
#> $folds$`5`
#> [1] 74 38 46 80 47 78 10 45 51 28 61 79 58 17 52 59
#>
#>
#> $lambda.min5
#> [1] 5
#>
#> $lambda.1se5
#> [1] 0DKplsRcox
DKplsRcox(X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5)
#> Kernel : rbfdot
#> Estimated_sigma 0.0122308
#> Error in model.matrix(mt0, mf0, contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
DKplsRcox(~X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5)
#> Error in model.matrix(mt0, mf0, , contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
DKplsRcox(Xplan=X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5,sparse=TRUE, alpha.pvals.expli=.15)
#> Kernel : rbfdot
#> Estimated_sigma 0.01203267
#> Error in model.matrix(mt0, mf0, contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut
DKplsRcox(Xplan=~X_train_micro,time=Y_train_micro,event=C_train_micro,nt=5,sparse=TRUE, alpha.pvals.expli=.15)
#> Error in model.matrix(mt0, mf0, , contrasts.arg = contrasts.arg): l'argument "contrasts.arg" est manquant, avec aucune valeur par défaut

