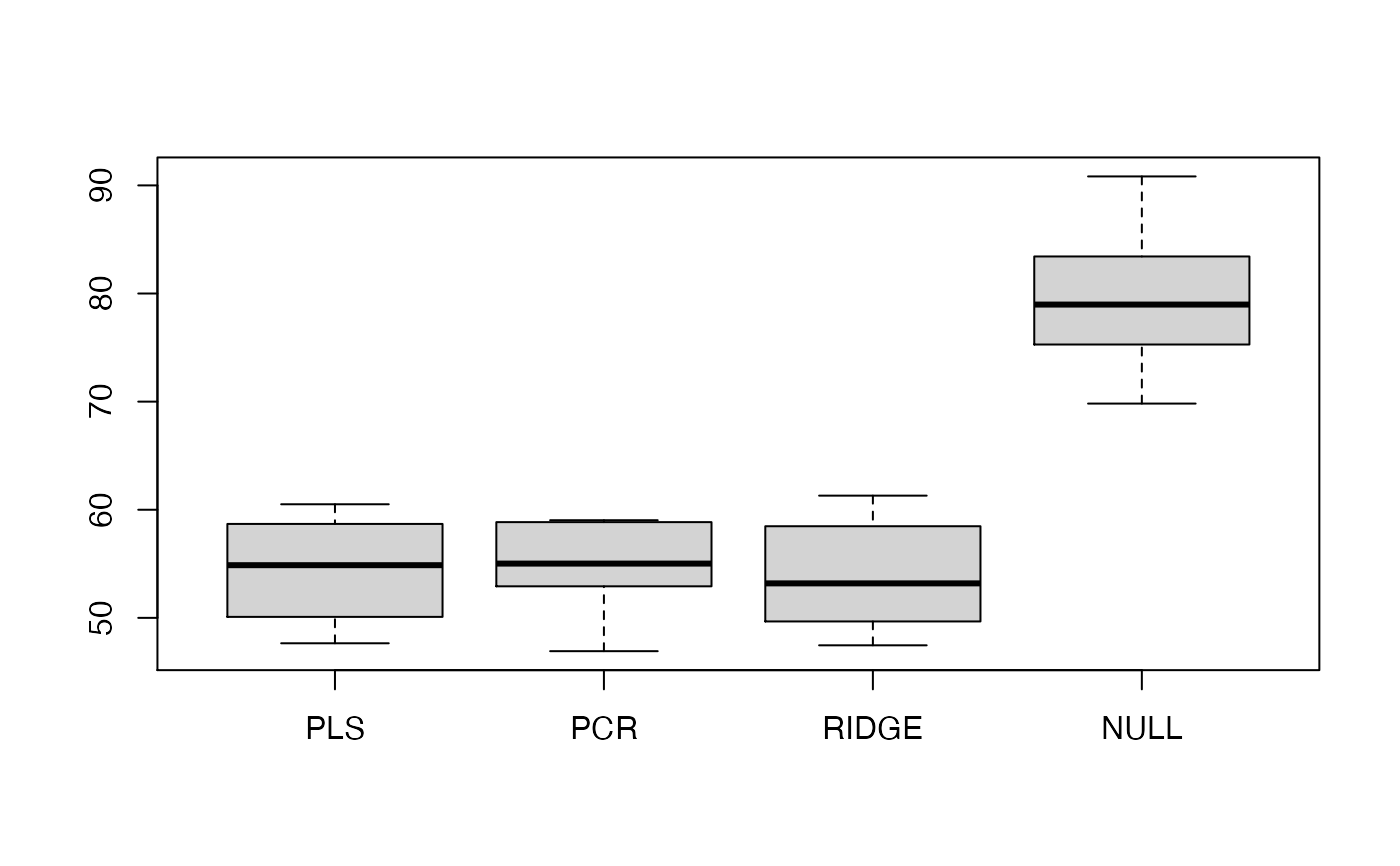
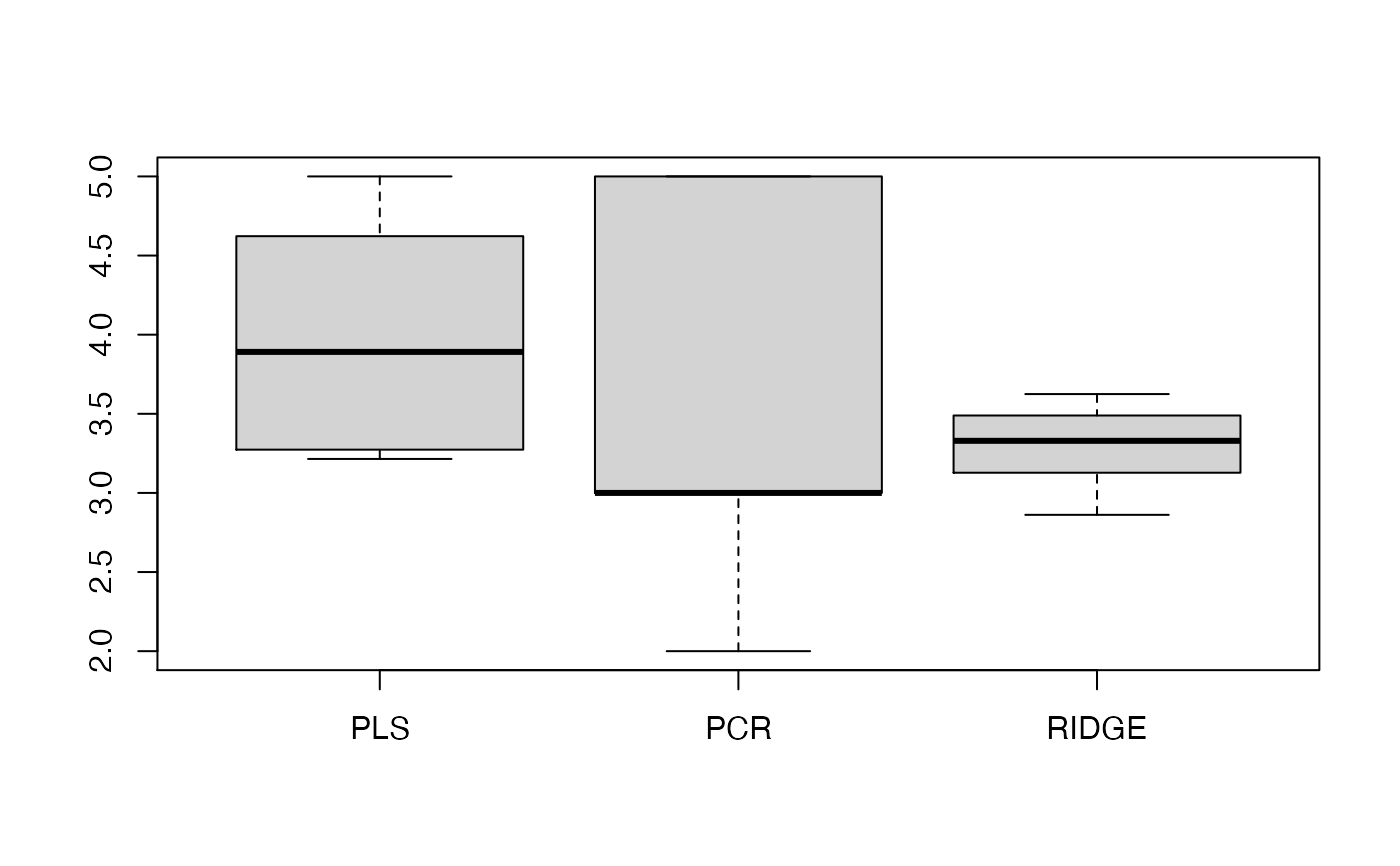
Comparison of Partial Least Squares Regression, Principal Components Regression and Ridge Regression.

Source: R/benchmark.regression.R

This function computes the test error over several runs for (a) PLS, (b) PCR (c) Ridge Regression and (d) the null model, that is the mean of y. In the first three cases, the optimal model is selected via cross-validation.

benchmark.regression(
  X,
  y,
  m = ncol(X),
  R = 20,
  ratio = 0.8,
  verbose = TRUE,
  k = 10,
  nsamples = nrow(X),
  use.kernel = FALSE,
  supervised = FALSE
)

Arguments

X

matrix of predictor observations.
y

vector of response observations. The length of y is the same as the number of rows of X.
m

maximal number of components for PLS. Default is m=ncol(X).
R

number of runs. Default is 20.
ratio

ratio no of training examples/(no of training examples + no of test examples). Default is 0.8
verbose

If TRUE, the functions plots the progress of the function. Default is TRUE.
k

number of cross-validation splits. Default is 10.
nsamples

number of data points. Default is nrow(X).
use.kernel

Use kernel representation for PLS? Default is use.kernel=FALSE.
supervised

Should the principal components be sorted by decreasing squared correlation to the response? Default is FALSE.

Value

MSE

data frame of size R x 4. It contains the test error for the four different methods for each of the R runs.

M

data frame of size R x 4. It contains the optimal model parameters for the four different methods for each of the R runs.

DoF

data frame of size R x 4. It contains the Degrees of Freedom (corresponding to M) for the four different methods for each of the R runs.

res.pls

matrix of size R x (ncol(X+1)). It contains the SSR for PLS for each of the R runs.

res.pcr

matrix of size R x (ncol(X+1)). It contains the SSR for PCR for each of the R runs.

DoF.all

matrix of size R x (ncol(X+1)). It contains the Degrees of Freedom for PLS for all components for each of the R runs.

Details

The function computes the test error, the cross-validation-optimal model parameters, their corresponding Degrees of Freedom, and the sum-of-squared-residuals (SSR) for PLS and PCR.

References

Kraemer, N., Sugiyama M. (2011). "The Degrees of Freedom of Partial Least Squares Regression". Journal of the American Statistical Association 106 (494) https://www.tandfonline.com/doi/abs/10.1198/jasa.2011.tm10107

See also

pls.cv, pcr.cv, benchmark.pls

Author

Nicole Kraemer

Examples


# \donttest{
# Boston Housing data
library(MASS)
data(Boston)
X<-as.matrix(Boston[,1:4]) # select the first 3 columns as predictor variables
y<-as.vector(Boston[,14])

my.benchmark<-benchmark.regression(X,y,ratio=0.5,R=10,k=5)

#> iteration no  1  
#> iteration no  2  
#> iteration no  3  
#> iteration no  4  
#> iteration no  5  
#> iteration no  6  
#> iteration no  7  
#> iteration no  8  
#> iteration no  9  
#> iteration no  10  

# boxplot of the mean squared error

boxplot(my.benchmark$MSE,outline=FALSE)


# boxplot of the degrees of freedom, without the null model

boxplot(my.benchmark$DoF[,-4])

# }