Degrees of Freedom and Statistical Inference for Partial Least Squares Regression

Source: R/plsdof-package.R

The plsdof package provides Degrees of Freedom estimates for Partial Least Squares (PLS) Regression.

Details

Model selection for PLS is based on various information criteria (aic, bic, gmdl) or on cross-validation. Estimates for the mean and covariance of the PLS regression coefficients are available. They allow the construction of approximate confidence intervals and the application of test procedures.

Further, cross-validation procedures for Ridge Regression and Principal Components Regression are available.

Package:plsdof
Type:Package
Version:0.2-9
Date:2019-31-01
License:GPL (>=2)
LazyLoad:yes

References

Kraemer, N., Sugiyama M. (2011). "The Degrees of Freedom of Partial Least Squares Regression". Journal of the American Statistical Association 106 (494) https://www.tandfonline.com/doi/abs/10.1198/jasa.2011.tm10107

Kraemer, N., Braun, M.L. (2007) "Kernelizing PLS, Degrees of Freedom, and Efficient Model Selection", Proceedings of the 24th International Conference on Machine Learning, Omni Press, 441 - 448

See also

pls.model, pls.cv, pls.ic

Author

Nicole Kraemer, Mikio L. Braun

Maintainer: Frederic Bertrand <frederic.bertrand@utt.fr.fr>

Examples


# Boston Housing data
data(Boston)
X<-as.matrix(Boston[,-14])
y<-as.vector(Boston[,14])

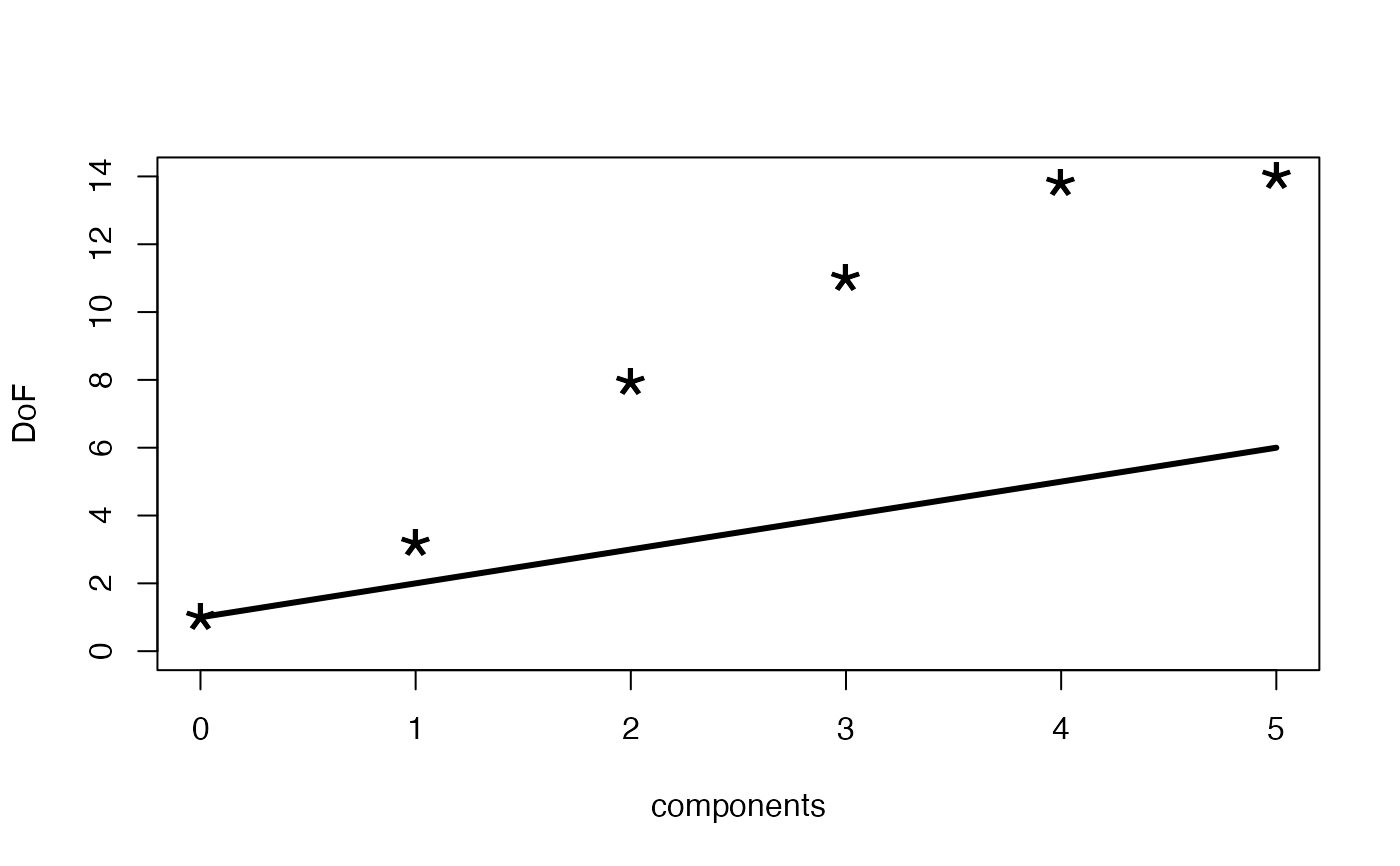
# compute PLS coefficients for the first 5 components and plot Degrees of Freedom

my.pls1<-pls.model(X,y,m=5,compute.DoF=TRUE)

plot(0:5,my.pls1$DoF,pch="*",cex=3,xlab="components",ylab="DoF",ylim=c(0,14))

# add naive estimate
lines(0:5,1:6,lwd=3)


# model selection with the Bayesian Information criterion

mypls2<-pls.ic(X,y,criterion="bic")

# model selection based on cross-validation. 
# returns the estimated covariance matrix of the regression coefficients

mypls3<-pls.cv(X,y,compute.covariance=TRUE)
my.vcov<-vcov(mypls3)
my.sd<-sqrt(diag(my.vcov)) # standard deviation of the regression coefficients