Cross-validating a larsDR-Model

This function cross-validates larsDR_coxph models.

cv.larsDR(
  data,
  method = c("efron", "breslow"),
  nfold = 5,
  fraction = seq(0, 1, length = 100),
  plot.it = TRUE,
  se = TRUE,
  givefold,
  scaleX = TRUE,
  scaleY = FALSE,
  folddetails = FALSE,
  allCVcrit = FALSE,
  details = FALSE,
  namedataset = "data",
  save = FALSE,
  verbose = TRUE,
  ...
)

Arguments

data

A list of three items:

x the explanatory variables passed to larsDR_coxph's Xplan argument,
time passed to larsDR_coxph's time argument,
status larsDR_coxph's status argument.

method

A character string specifying the method for tie handling. If there are no tied death times all the methods are equivalent. The Efron approximation is used as the default here, it is more accurate when dealing with tied death times, and is as efficient computationally.

nfold

The number of folds to use to perform the cross-validation process.

fraction

L1 norm fraction.

plot.it

Shall the results be displayed on a plot ?

se

Should standard errors be plotted ?

givefold

Explicit list of omited values in each fold can be provided using this argument.

scaleX

Shall the predictors be standardized ?

scaleY

Should the time values be standardized ?

folddetails

Should values and completion status for each folds be returned ?

allCVcrit

Should the other 13 CV criteria be evaled and returned ?

details

Should all results of the functions that perform error computations be returned ?

namedataset

Name to use to craft temporary results names

save

Should temporary results be saved ?

verbose

Should some CV details be displayed ?

...

Other arguments to pass to larsDR_coxph.

Value

nt: The number of components requested
cv.error1: Vector with the mean values, across folds, of, per fold unit, Cross-validated log-partial-likelihood for models with 0 to nt components.
cv.error2: Vector with the mean values, across folds, of, per fold unit, van Houwelingen Cross-validated log-partial-likelihood for models with 0 to nt components.
cv.error3: Vector with the mean values, across folds, of iAUC_CD for models with 0 to nt components.
cv.error4: Vector with the mean values, across folds, of iAUC_hc for models with 0 to nt components.
cv.error5: Vector with the mean values, across folds, of iAUC_sh for models with 0 to nt components.
cv.error6: Vector with the mean values, across folds, of iAUC_Uno for models with 0 to nt components.
cv.error7: Vector with the mean values, across folds, of iAUC_hz.train for models with 0 to nt components.
cv.error8: Vector with the mean values, across folds, of iAUC_hz.test for models with 0 to nt components.
cv.error9: Vector with the mean values, across folds, of iAUC_survivalROC.train for models with 0 to nt components.
cv.error10: Vector with the mean values, across folds, of iAUC_survivalROC.test for models with 0 to nt components.
cv.error11: Vector with the mean values, across folds, of iBrierScore unw for models with 0 to nt components.
cv.error12: Vector with the mean values, across folds, of iSchmidScore (robust BS) unw for models with 0 to nt components.
cv.error13: Vector with the mean values, across folds, of iBrierScore w for models with 0 to nt components.
cv.error14: Vector with the mean values, across folds, of iSchmidScore (robust BS) w for models with 0 to nt components.
cv.se1: Vector with the standard error values, across folds, of, per fold unit, Cross-validated log-partial-likelihood for models with 0 to nt components.
cv.se2: Vector with the standard error values, across folds, of, per fold unit, van Houwelingen Cross-validated log-partial-likelihood for models with 0 to nt components.
cv.se3: Vector with the standard error values, across folds, of iAUC_CD for models with 0 to nt components.
cv.se4: Vector with the standard error values, across folds, of iAUC_hc for models with 0 to nt components.
cv.se5: Vector with the standard error values, across folds, of iAUC_sh for models with 0 to nt components.
cv.se6: Vector with the standard error values, across folds, of iAUC_Uno for models with 0 to nt components.
cv.se7: Vector with the standard error values, across folds, of iAUC_hz.train for models with 0 to nt components.
cv.se8: Vector with the standard error values, across folds, of iAUC_hz.test for models with 0 to nt components.
cv.se9: Vector with the standard error values, across folds, of iAUC_survivalROC.train for models with 0 to nt components.
cv.se10: Vector with the standard error values, across folds, of iAUC_survivalROC.test for models with 0 to nt components.
cv.se11: Vector with the standard error values, across folds, of iBrierScore unw for models with 0 to nt components.
cv.se12: Vector with the standard error values, across folds, of iSchmidScore (robust BS) unw for models with 0 to nt components.
cv.se13: Vector with the standard error values, across folds, of iBrierScore w for models with 0 to nt components.
cv.se14: Vector with the standard error values, across folds, of iSchmidScore (robust BS) w for models with 0 to nt components.
folds: Explicit list of the values that were omited values in each fold.
lambda.min1: Vector with the standard error values, across folds, of, per fold unit, Cross-validated log-partial-likelihood for models with 0 to nt components.
lambda.min2: Vector with the standard error values, across folds, of, per fold unit, van Houwelingen Cross-validated log-partial-likelihood for models with 0 to nt components.
lambda.min1: Optimal Nbr of components, min Cross-validated log-partial-likelihood criterion.
lambda.se1: Optimal Nbr of components, min+1se Cross-validated log-partial-likelihood criterion.
lambda.min2: Optimal Nbr of components, min van Houwelingen Cross-validated log-partial-likelihood.
lambda.se2: Optimal Nbr of components, min+1se van Houwelingen Cross-validated log-partial-likelihood.
lambda.min3: Optimal Nbr of components, max iAUC_CD criterion.
lambda.se3: Optimal Nbr of components, max+1se iAUC_CD criterion.
lambda.min4: Optimal Nbr of components, max iAUC_hc criterion.
lambda.se4: Optimal Nbr of components, max+1se iAUC_hc criterion.
lambda.min5: Optimal Nbr of components, max iAUC_sh criterion.
lambda.se5: Optimal Nbr of components, max+1se iAUC_sh criterion.
lambda.min6: Optimal Nbr of components, max iAUC_Uno criterion.
lambda.se6: Optimal Nbr of components, max+1se iAUC_Uno criterion.
lambda.min7: Optimal Nbr of components, max iAUC_hz.train criterion.
lambda.se7: Optimal Nbr of components, max+1se iAUC_hz.train criterion.
lambda.min8: Optimal Nbr of components, max iAUC_hz.test criterion.
lambda.se8: Optimal Nbr of components, max+1se iAUC_hz.test criterion.
lambda.min9: Optimal Nbr of components, max iAUC_survivalROC.train criterion.
lambda.se9: Optimal Nbr of components, max+1se iAUC_survivalROC.train criterion.
lambda.min10: Optimal Nbr of components, max iAUC_survivalROC.test criterion.
lambda.se10: Optimal Nbr of components, max+1se iAUC_survivalROC.test criterion.
lambda.min11: Optimal Nbr of components, min iBrierScore unw criterion.
lambda.se11: Optimal Nbr of components, min+1se iBrierScore unw criterion.
lambda.min12: Optimal Nbr of components, min iSchmidScore unw criterion.
lambda.se12: Optimal Nbr of components, min+1se iSchmidScore unw criterion.
lambda.min13: Optimal Nbr of components, min iBrierScore w criterion.
lambda.se13: Optimal Nbr of components, min+1se iBrierScore w criterion.
lambda.min14: Optimal Nbr of components, min iSchmidScore w criterion.
lambda.se14: Optimal Nbr of components, min+1se iSchmidScore w criterion.
errormat1-14: If details=TRUE, matrices with the error values for every folds across each of the components and each of the criteria
completed.cv1-14: If details=TRUE, matrices with logical values for every folds across each of the components and each of the criteria: TRUE if the computation was completed and FALSE it is failed.
larsmodfull: Lars model fitted on the residuals.
All_indics: All results of the functions that perform error computation, for each fold, each component and error criterion.

Details

It only computes the recommended van Houwelingen CV partial likelihood criterion criterion. Set allCVcrit=TRUE to retrieve the 13 other ones.

References

plsRcox, Cox-Models in a high dimensional setting in R, Frederic Bertrand, Philippe Bastien, Nicolas Meyer and Myriam Maumy-Bertrand (2014). Proceedings of User2014!, Los Angeles, page 152.

Deviance residuals-based sparse PLS and sparse kernel PLS regression for censored data, Philippe Bastien, Frederic Bertrand, Nicolas Meyer and Myriam Maumy-Bertrand (2015), Bioinformatics, 31(3):397-404, doi:10.1093/bioinformatics/btu660.

Author

Frédéric Bertrand
frederic.bertrand@utt.fr
http://www-irma.u-strasbg.fr/~fbertran/

Examples


data(micro.censure)
data(Xmicro.censure_compl_imp)
set.seed(123456)
X_train_micro <- apply((as.matrix(Xmicro.censure_compl_imp)),FUN="as.numeric",MARGIN=2)[1:80,]
X_train_micro_df <- data.frame(X_train_micro)
Y_train_micro <- micro.censure$survyear[1:80]
C_train_micro <- micro.censure$DC[1:80]

#Should be run with the default: fraction = seq(0, 1, length = 100)
(cv.larsDR.res=cv.larsDR(list(x=X_train_micro,time=Y_train_micro,
status=C_train_micro),se=TRUE,fraction=seq(0, 1, length = 4)))
#> CV Fold 1 
#> CV Fold 2 
#> CV Fold 3 
#> CV Fold 4 
#> CV Fold 5 

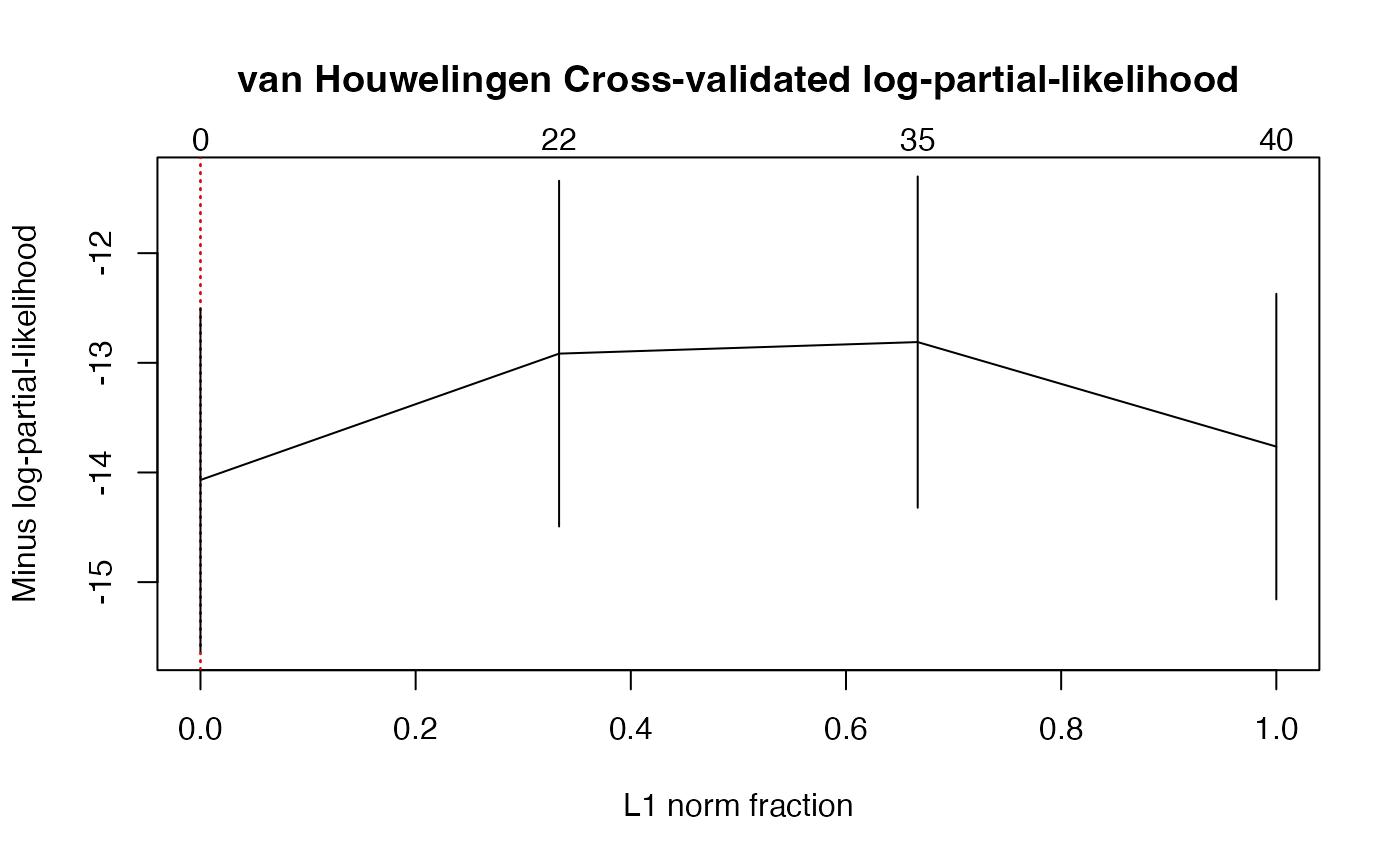#> $fraction
#> [1] 0.0000000 0.3333333 0.6666667 1.0000000
#> 
#> $cv.error2
#> [1] -14.06841 -12.91622 -12.81085 -13.76411
#> 
#> $cv.se2
#> [1] 1.561171 1.576406 1.510617 1.393355
#> 
#> $folds
#> $folds$`1`
#>  [1] 60  3  2 14 77  6 50  4 72 32 22  1 41 21 63 25
#> 
#> $folds$`2`
#>  [1] 42 67 65 15 73 48 57 26  7 13 31 53  5 27 37 64
#> 
#> $folds$`3`
#>  [1] 71 23 56 35 75 29 30 18 62 44 12 33 68 49 43 55
#> 
#> $folds$`4`
#>  [1] 54 76 24 16 34 66  9 11 69 40 70 36 39  8 19 20
#> 
#> $folds$`5`
#>  [1] 74 38 46 80 47 78 10 45 51 28 61 79 58 17 52 59
#> 
#> 
#> $lambda.min2
#> [1] 0
#> 
#> $lambda.1se2
#> [1] 0
#> 
#> $nzb
#> [1]  0 22 35 40
#> 
#> $larsmodfull
#> 
#> Call:
#> lars(x = x, y = DR_coxph, type = "lasso", use.Gram = FALSE)
#> R-squared: 0.689 
#> Sequence of LASSO moves:
#>       N D3S1282 D16S408 D20S107 D15S127 D2S138 Agediag D1S207 D22S928 D10S191
#> Var  38      12      31       4      13     16      35     15       9      19
#> Step  1       2       3       4       5      6       7      8       9      10
#>      D5S346 D16S422  T D4S414 D1S225 D17S790 Siege D3S1283 sexe D1S305  M
#> Var       8      17 37     27     11      24    36      26   34     14 39
#> Step     11      12 13     14     15      16    17      18   19     20 21
#>      D8S283 D14S65 D17S794 TP53 D9S171 D13S173 D2S159 D4S394 D6S264 D16S408
#> Var      28     23       2    5      6       3     30     20     22     -31
#> Step     22     23      24   25     26      27     28     29     30      31
#>      D5S430 D8S264 D18S61 D1S197 D11S916 D6S275 D16S408 TP53 D10S192 sexe
#> Var      25      7      1     21      29     32      31   -5      33  -34
#> Step     32     33     34     35      36     37      38   39      40   41
#>      D9S179 TP53 sexe STADE D8S264 D18S53 D8S264 D17S794 D17S794
#> Var      18    5   34    40     -7     10      7      -2       2
#> Step     42   43   44    45     46     47     48      49      50
#>