Plot an object of class

Plot an object of class "Fa". If which = "factorScore", then a scatterplot of the factor scores is produced; if which = "screeplot", shows the eigenvalues and is helpful to select the number of factors.

Usage

# S4 method for class 'Fa'
plot(x, which=c("factorScore", "screeplot"), choices=1:2)

Arguments

x: an object of class "Fa" or of a class derived from "Fa"
which: indicate what kind of plot. If which = "factorScore", then a scatterplot of the factor scores is produced; if which = "screeplot", shows the eigenvalues and is helpful to select the number of factors.
choices: an integer vector indicate which columns of the factor scores to plot

Details

The feasible usages are: plot(x, which="factorScore", choices=1:2) plot(x, which="screeplot")

Methods

signature(x = "Fa", y = "missing"): generic functions - see plot

References

Zhang, Y. Y. (2013), An Object Oriented Solution for Robust Factor Analysis.

Author

Ying-Ying Zhang (Robert) robertzhangyying@qq.com

Examples


data("hbk")
hbk.x = hbk[,1:3] 

faClassicPcaReg = FaClassic(x = hbk.x, factors = 2, method = "pca",
scoresMethod = "regression"); faClassicPcaReg
#> An object of class "FaClassic"
#> Slot "call":
#> FaClassic(x = hbk.x, factors = 2, method = "pca", scoresMethod = "regression")
#> 
#> Slot "converged":
#> NULL
#> 
#> Slot "loadings":
#>      Factor1  Factor2
#> X1  3.411036 0.936662
#> X2  7.278529 3.860723
#> X3 11.270812 3.273734
#> 
#> Slot "communality":
#>        X1        X2        X3 
#>  12.51250  67.88217 137.74853 
#> 
#> Slot "uniquenesses":
#>           X1           X2           X3 
#> 0.8292095832 0.0007959085 0.0863235416 
#> 
#> Slot "cor":
#> [1] FALSE
#> 
#> Slot "covariance":
#>          X1       X2        X3
#> X1 13.34171 28.46921  41.24398
#> X2 28.46921 67.88297  94.66562
#> X3 41.24398 94.66562 137.83486
#> 
#> Slot "correlation":
#>           X1        X2        X3
#> X1 1.0000000 0.9459958 0.9617790
#> X2 0.9459958 1.0000000 0.9786612
#> X3 0.9617790 0.9786612 1.0000000
#> 
#> Slot "usedMatrix":
#>          X1       X2        X3
#> X1 13.34171 28.46921  41.24398
#> X2 28.46921 67.88297  94.66562
#> X3 41.24398 94.66562 137.83486
#> 
#> Slot "reducedCorrelation":
#> NULL
#> 
#> Slot "criteria":
#> NULL
#> 
#> Slot "factors":
#> [1] 2
#> 
#> Slot "dof":
#> NULL
#> 
#> Slot "method":
#> [1] "pca"
#> 
#> Slot "scores":
#>            Factor1      Factor2
#>  [1,]  1.836216178  0.161337548
#>  [2,]  1.756800683  0.549735006
#>  [3,]  2.250318962 -0.462115084
#>  [4,]  2.110379324  0.145591275
#>  [5,]  2.095218367  0.066345803
#>  [6,]  1.906582805  0.232737572
#>  [7,]  1.788199906  0.587263155
#>  [8,]  1.911901278  0.021274118
#>  [9,]  2.106202931 -0.053757894
#> [10,]  2.122518267 -0.342046036
#> [11,]  2.348800415  0.342830312
#> [12,]  2.927387983 -1.009336488
#> [13,]  1.905818664  1.685956006
#> [14,]  0.528829255  6.359573459
#> [15,] -0.448347445  0.133780216
#> [16,] -0.668908585  0.366404244
#> [17,] -0.779858578  0.442576537
#> [18,] -0.320380311 -0.436151460
#> [19,] -0.697421067  0.621061863
#> [20,] -0.531502346  0.422359906
#> [21,] -0.418046839 -0.099159644
#> [22,] -0.718663795  0.742356037
#> [23,] -0.665393822  0.394816805
#> [24,] -0.761582949  0.580540198
#> [25,] -0.419693120 -0.657298051
#> [26,] -0.598455877  0.539385243
#> [27,] -0.247874654 -0.345083251
#> [28,] -0.219836054 -0.829109302
#> [29,] -0.484797036 -0.302159906
#> [30,]  0.006043560 -1.273196784
#> [31,] -0.414104099 -0.319367475
#> [32,] -0.862788836  0.802561432
#> [33,] -0.704564559  0.680970529
#> [34,] -0.404005807 -0.681812987
#> [35,] -0.226207238 -0.410125033
#> [36,] -0.370021556 -0.176933456
#> [37,] -0.581066520  0.435007090
#> [38,] -0.621218623  0.029086231
#> [39,] -0.210664210 -1.057488778
#> [40,] -0.638509599  0.278324368
#> [41,] -0.093737402 -0.869315133
#> [42,] -0.222301393 -0.760169894
#> [43,] -0.929819437  1.166157588
#> [44,]  0.040846868 -1.395395068
#> [45,] -0.345171409 -0.777979662
#> [46,]  0.005618871 -1.329449176
#> [47,] -0.241826492 -0.980332711
#> [48,] -0.094700744 -0.865086128
#> [49,] -0.436399538  0.009447513
#> [50,] -0.371498956 -0.025665034
#> [51,] -0.585765982  0.034545544
#> [52,] -0.234984713 -0.865075764
#> [53,] -0.017987529 -1.299228393
#> [54,] -0.924264023  1.069378350
#> [55,] -0.757104843  0.604723754
#> [56,] -0.808109523  0.898476392
#> [57,] -0.432379728 -0.457331137
#> [58,] -0.698147469  0.739975084
#> [59,] -0.269779011 -0.394725685
#> [60,] -0.198808958 -0.673656887
#> [61,] -0.557786430  0.493393901
#> [62,] -0.459937878 -0.555054318
#> [63,] -0.892563087  0.931740886
#> [64,] -0.361028449  0.001270686
#> [65,] -0.067714855 -1.141591364
#> [66,] -0.694666313  0.333677831
#> [67,] -0.570392680  0.141917212
#> [68,] -0.352127153 -0.776502820
#> [69,] -0.474012517 -0.407110790
#> [70,] -0.340986005 -0.230478698
#> [71,] -0.421675567 -0.010838417
#> [72,] -0.579475155  0.167004879
#> [73,] -0.425439569 -0.197214204
#> [74,] -0.631892463  0.322176109
#> [75,] -0.141285522 -1.068417769
#> 
#> Slot "scoresMethod":
#> [1] "regression"
#> 
#> Slot "scoringCoef":
#>                  X1         X2         X3
#> Factor1  0.06192447 -0.1643831  0.1761400
#> Factor2 -0.12400651  0.5687014 -0.3297295
#> 
#> Slot "meanF":
#>       Factor1       Factor2 
#>  1.473636e-15 -2.560914e-15 
#> 
#> Slot "corF":
#>              Factor1      Factor2
#> Factor1 1.000000e+00 5.144533e-15
#> Factor2 5.144533e-15 1.000000e+00
#> 
#> Slot "STATISTIC":
#> NULL
#> 
#> Slot "PVAL":
#> NULL
#> 
#> Slot "n.obs":
#> [1] 75
#> 
#> Slot "center":
#>       X1       X2       X3 
#> 3.206667 5.597333 7.230667 
#> 
#> Slot "eigenvalues":
#> [1] 216.162129   1.981077   0.916329
#> 
#> Slot "cov.control":
#> NULL
#> 
summary(faClassicPcaReg)
#> An object of class "SummaryFa"
#> Slot "faobj":
#> An object of class "FaClassic"
#> Slot "call":
#> FaClassic(x = hbk.x, factors = 2, method = "pca", scoresMethod = "regression")
#> 
#> Slot "converged":
#> NULL
#> 
#> Slot "loadings":
#>      Factor1  Factor2
#> X1  3.411036 0.936662
#> X2  7.278529 3.860723
#> X3 11.270812 3.273734
#> 
#> Slot "communality":
#>        X1        X2        X3 
#>  12.51250  67.88217 137.74853 
#> 
#> Slot "uniquenesses":
#>           X1           X2           X3 
#> 0.8292095832 0.0007959085 0.0863235416 
#> 
#> Slot "cor":
#> [1] FALSE
#> 
#> Slot "covariance":
#>          X1       X2        X3
#> X1 13.34171 28.46921  41.24398
#> X2 28.46921 67.88297  94.66562
#> X3 41.24398 94.66562 137.83486
#> 
#> Slot "correlation":
#>           X1        X2        X3
#> X1 1.0000000 0.9459958 0.9617790
#> X2 0.9459958 1.0000000 0.9786612
#> X3 0.9617790 0.9786612 1.0000000
#> 
#> Slot "usedMatrix":
#>          X1       X2        X3
#> X1 13.34171 28.46921  41.24398
#> X2 28.46921 67.88297  94.66562
#> X3 41.24398 94.66562 137.83486
#> 
#> Slot "reducedCorrelation":
#> NULL
#> 
#> Slot "criteria":
#> NULL
#> 
#> Slot "factors":
#> [1] 2
#> 
#> Slot "dof":
#> NULL
#> 
#> Slot "method":
#> [1] "pca"
#> 
#> Slot "scores":
#>            Factor1      Factor2
#>  [1,]  1.836216178  0.161337548
#>  [2,]  1.756800683  0.549735006
#>  [3,]  2.250318962 -0.462115084
#>  [4,]  2.110379324  0.145591275
#>  [5,]  2.095218367  0.066345803
#>  [6,]  1.906582805  0.232737572
#>  [7,]  1.788199906  0.587263155
#>  [8,]  1.911901278  0.021274118
#>  [9,]  2.106202931 -0.053757894
#> [10,]  2.122518267 -0.342046036
#> [11,]  2.348800415  0.342830312
#> [12,]  2.927387983 -1.009336488
#> [13,]  1.905818664  1.685956006
#> [14,]  0.528829255  6.359573459
#> [15,] -0.448347445  0.133780216
#> [16,] -0.668908585  0.366404244
#> [17,] -0.779858578  0.442576537
#> [18,] -0.320380311 -0.436151460
#> [19,] -0.697421067  0.621061863
#> [20,] -0.531502346  0.422359906
#> [21,] -0.418046839 -0.099159644
#> [22,] -0.718663795  0.742356037
#> [23,] -0.665393822  0.394816805
#> [24,] -0.761582949  0.580540198
#> [25,] -0.419693120 -0.657298051
#> [26,] -0.598455877  0.539385243
#> [27,] -0.247874654 -0.345083251
#> [28,] -0.219836054 -0.829109302
#> [29,] -0.484797036 -0.302159906
#> [30,]  0.006043560 -1.273196784
#> [31,] -0.414104099 -0.319367475
#> [32,] -0.862788836  0.802561432
#> [33,] -0.704564559  0.680970529
#> [34,] -0.404005807 -0.681812987
#> [35,] -0.226207238 -0.410125033
#> [36,] -0.370021556 -0.176933456
#> [37,] -0.581066520  0.435007090
#> [38,] -0.621218623  0.029086231
#> [39,] -0.210664210 -1.057488778
#> [40,] -0.638509599  0.278324368
#> [41,] -0.093737402 -0.869315133
#> [42,] -0.222301393 -0.760169894
#> [43,] -0.929819437  1.166157588
#> [44,]  0.040846868 -1.395395068
#> [45,] -0.345171409 -0.777979662
#> [46,]  0.005618871 -1.329449176
#> [47,] -0.241826492 -0.980332711
#> [48,] -0.094700744 -0.865086128
#> [49,] -0.436399538  0.009447513
#> [50,] -0.371498956 -0.025665034
#> [51,] -0.585765982  0.034545544
#> [52,] -0.234984713 -0.865075764
#> [53,] -0.017987529 -1.299228393
#> [54,] -0.924264023  1.069378350
#> [55,] -0.757104843  0.604723754
#> [56,] -0.808109523  0.898476392
#> [57,] -0.432379728 -0.457331137
#> [58,] -0.698147469  0.739975084
#> [59,] -0.269779011 -0.394725685
#> [60,] -0.198808958 -0.673656887
#> [61,] -0.557786430  0.493393901
#> [62,] -0.459937878 -0.555054318
#> [63,] -0.892563087  0.931740886
#> [64,] -0.361028449  0.001270686
#> [65,] -0.067714855 -1.141591364
#> [66,] -0.694666313  0.333677831
#> [67,] -0.570392680  0.141917212
#> [68,] -0.352127153 -0.776502820
#> [69,] -0.474012517 -0.407110790
#> [70,] -0.340986005 -0.230478698
#> [71,] -0.421675567 -0.010838417
#> [72,] -0.579475155  0.167004879
#> [73,] -0.425439569 -0.197214204
#> [74,] -0.631892463  0.322176109
#> [75,] -0.141285522 -1.068417769
#> 
#> Slot "scoresMethod":
#> [1] "regression"
#> 
#> Slot "scoringCoef":
#>                  X1         X2         X3
#> Factor1  0.06192447 -0.1643831  0.1761400
#> Factor2 -0.12400651  0.5687014 -0.3297295
#> 
#> Slot "meanF":
#>       Factor1       Factor2 
#>  1.473636e-15 -2.560914e-15 
#> 
#> Slot "corF":
#>              Factor1      Factor2
#> Factor1 1.000000e+00 5.144533e-15
#> Factor2 5.144533e-15 1.000000e+00
#> 
#> Slot "STATISTIC":
#> NULL
#> 
#> Slot "PVAL":
#> NULL
#> 
#> Slot "n.obs":
#> [1] 75
#> 
#> Slot "center":
#>       X1       X2       X3 
#> 3.206667 5.597333 7.230667 
#> 
#> Slot "eigenvalues":
#> [1] 216.162129   1.981077   0.916329
#> 
#> Slot "cov.control":
#> NULL
#> 
#> 
#> Slot "importance":
#>                Factor1 Factor2
#> SS loadings    191.643  26.500
#> Proportion Var   0.875   0.121
#> Cumulative Var   0.875   0.996
#> 

plot(faClassicPcaReg, which = "factorScore", choices = 1:2)

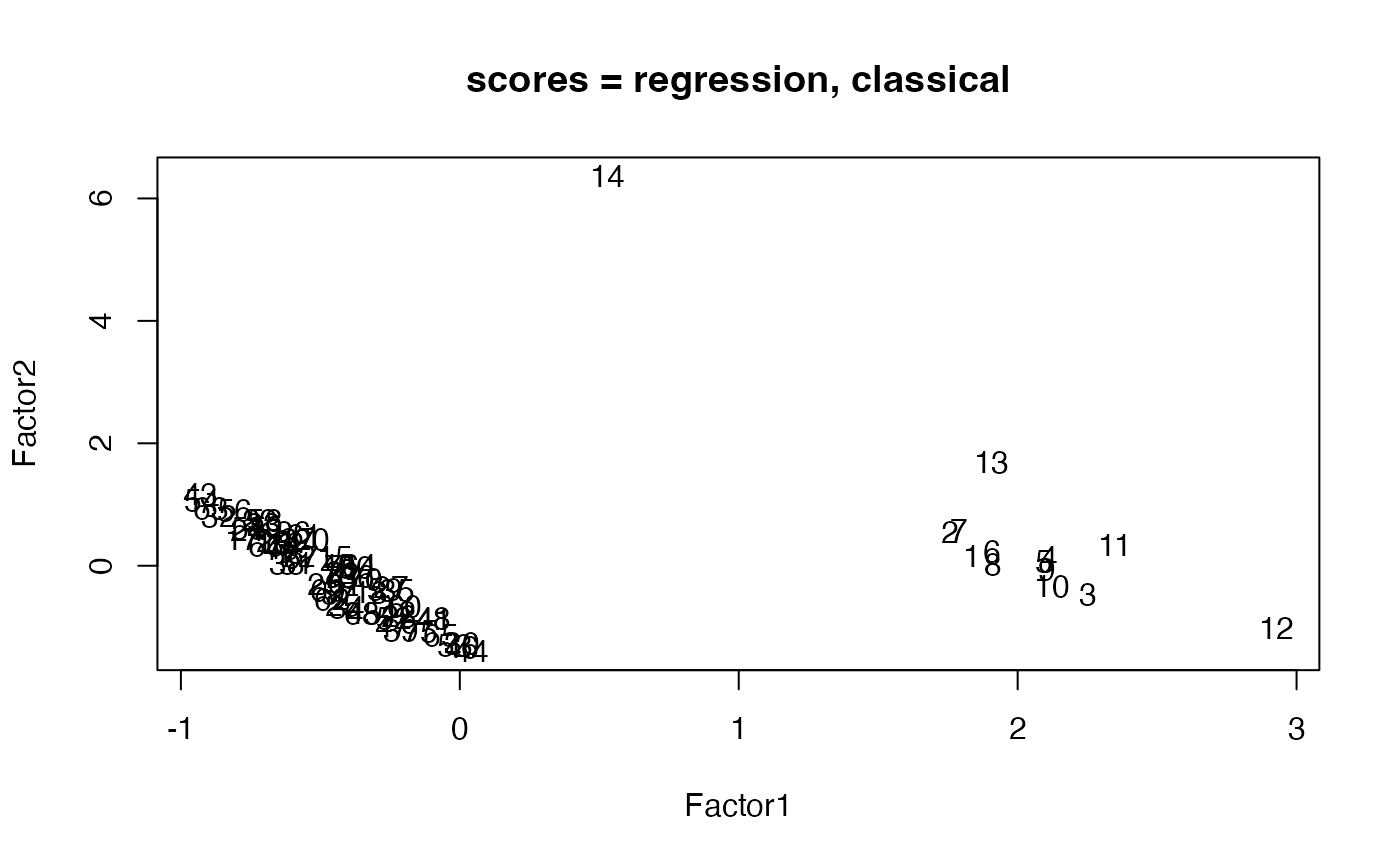plot(faClassicPcaReg, which = "screeplot")