Data generating function for univariate gamma plsR models

Source: R/simul_data_UniYX_gamma.R

This function generates a single univariate gamma response value \(Ygamma\) and a vector of explanatory variables \((X_1,\ldots,X_{totdim})\) drawn from a model with a given number of latent components.

simul_data_UniYX_gamma(totdim, ncomp, jvar, lvar, link = "inverse", offset = 0)

Arguments

totdim

Number of columns of the X vector (from ncomp to hardware limits)
ncomp

Number of latent components in the model (to use noise, select ncomp=3)
jvar

First variance parameter
lvar

Second variance parameter
link

Character specification of the link function in the mean model (mu). Currently, "inverse", "log" and "identity" are supported. Alternatively, an object of class "link-glm" can be supplied.
offset

Offset on the linear scale

Value

vector

\((Ygamma,X_1,\ldots,X_{totdim})\)

Details

This function should be combined with the replicate function to give rise to a larger dataset. The algorithm used is a modification of a port of the one described in the article of Li which is a multivariate generalization of the algorithm of Naes and Martens.

References

T. Naes, H. Martens, Comparison of prediction methods for multicollinear data, Commun. Stat., Simul. 14 (1985) 545-576.
Morris, Elaine B. Martin, Model selection for partial least squares regression, Chemometrics and Intelligent Laboratory Systems 64 (2002), 79-89, doi: 10.1016/S0169-7439(02)00051-5 .

A new bootstrap-based stopping criterion in PLS component construction, J. Magnanensi, M. Maumy-Bertrand, N. Meyer and F. Bertrand (2016), in The Multiple Facets of Partial Least Squares and Related Methods, doi: 10.1007/978-3-319-40643-5_18

A new universal resample-stable bootstrap-based stopping criterion for PLS component construction, J. Magnanensi, F. Bertrand, M. Maumy-Bertrand and N. Meyer, (2017), Statistics and Computing, 27, 757–774. doi: 10.1007/s11222-016-9651-4

New developments in Sparse PLS regression, J. Magnanensi, M. Maumy-Bertrand, N. Meyer and F. Bertrand, (2021), Frontiers in Applied Mathematics and Statistics, doi: 10.3389/fams.2021.693126
.

See also

simul_data_UniYX

Author

Jeremy Magnanensi, Frédéric Bertrand
frederic.bertrand@utt.fr
https://fbertran.github.io/homepage/

Jérémy Magnanensi, Frédéric Bertrand
frederic.bertrand@utt.fr
https://fbertran.github.io/homepage/

Examples

set.seed(314)
ncomp=rep(3,100)
totdimpos=7:50
totdim=sample(totdimpos,100,replace=TRUE)
l=3.01
#for (l in seq(3.01,15.51,by=0.5)) {
j=3.01
#for (j in seq(3.01,9.51,by=0.5))  {
i=44
#for ( i in 1:100){
set.seed(i)
totdimi<-totdim[i]
ncompi<-ncomp[i]
datasim <- t(replicate(200,simul_data_UniYX_gamma(totdimi,ncompi,j,l)))
#}
#}
#}
pairs(datasim)

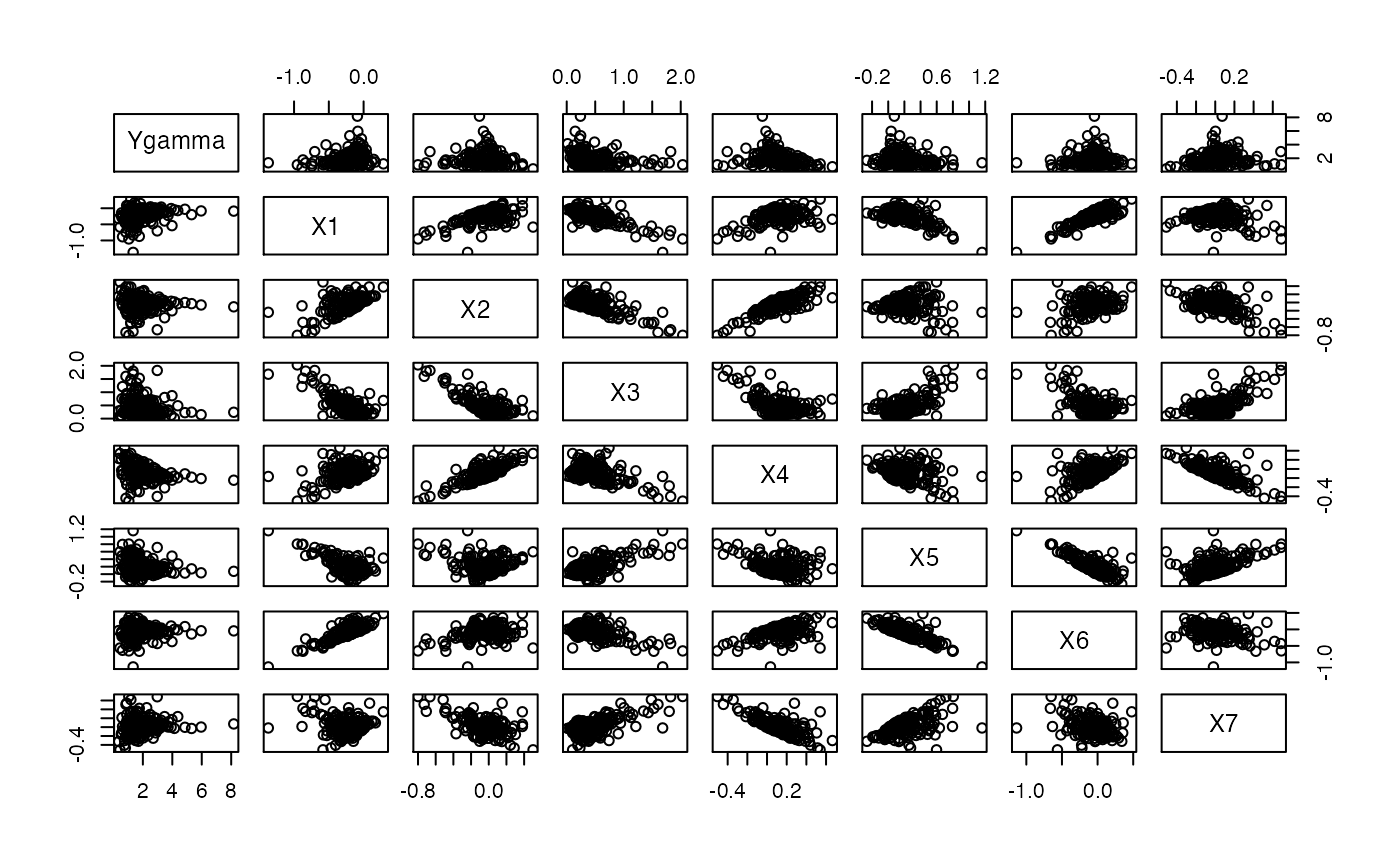rm(i,j,l,totdimi,ncompi,datasim)