bootPLS, using bootstrap to find hyperparameters for Partial Least Squares Regression models and their extensions

Frédéric Bertrand, Jeremy Magnanensi and Myriam Maumy-Bertrand

The goal of bootPLS is to provide several non-parametric stable bootstrap-based techniques to determine the numbers of components in Partial Least Squares and sparse Partial Least Squares linear or generalized linear regression.

bootPLS implements several algorithms that were published as a book chapter and two articles.

A new bootstrap-based stopping criterion in PLS component construction, J. Magnanensi, M. Maumy-Bertrand, N. Meyer and F. Bertrand (2016), in The Multiple Facets of Partial Least Squares and Related Methods, doi:10.1007/978-3-319-40643-5_18.
A new universal resample-stable bootstrap-based stopping criterion for PLS component construction, J. Magnanensi, F. Bertrand, M. Maumy-Bertrand and N. Meyer, (2017), Statistics and Computing, 27, 757–774. doi:10.1007/s11222-016-9651-4
New developments in Sparse PLS regression, J. Magnanensi, M. Maumy-Bertrand, N. Meyer and F. Bertrand, (2021), Frontiers in Applied Mathematics and Statistics, accepted.

Support for parallel computation and GPU is being developed.

This website and these examples were created by F. Bertrand and M. Maumy-Bertrand.

Installation

You can install the released version of bootPLS from CRAN with:

install.packages("bootPLS")

You can install the development version of bootPLS from github with:

devtools::install_github("fbertran/bootPLS")

Pine real dataset: pls and spls regressions

Loading and displaying dataset

Load and display the pinewood worm dataset.

library(bootPLS)
library(plsRglm)
data(pine, package = "plsRglm")
Xpine<-pine[,1:10]
ypine<-log(pine[,11])

pairs(pine)

Michel Tenenhaus’ reported in his book, La régression PLS (1998) Technip, Paris, that most of the expert biologists claimed that this dataset features two latent variables, which is tantamount to the PLS model having two components.

PLS LOO and CV

Leave one out CV (K=nrow(pine)) one time (NK=1).

bbb <- plsRglm::cv.plsR(log(x11)~.,data=pine,nt=6,K=nrow(pine),NK=1,verbose=FALSE)
plsRglm::cvtable(summary(bbb))
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Component____ 4 ____
#> ____Component____ 5 ____
#> ____Component____ 6 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> 
#> NK: 1
#> 
#> CV Q2 criterion:
#> 0 1 
#> 0 1 
#> 
#> CV Press criterion:
#> 1 2 3 4 5 
#> 0 0 0 0 1

Set up 6-fold CV (K=6), 100 times (NK=2), and use random=TRUE to randomly create folds for repeated CV.

bbb2 <- plsRglm::cv.plsR(log(x11)~.,data=pine,nt=6,K=6,NK=100,verbose=FALSE)

Display the results of the cross-validation.

plsRglm::cvtable(summary(bbb2))
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Component____ 4 ____
#> ____Component____ 5 ____
#> ____Component____ 6 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> 
#> NK: 1,  2,  3,  4,  5,  6,  7,  8,  9,  10
#> NK: 11,  12,  13,  14,  15,  16,  17,  18,  19,  20
#> NK: 21,  22,  23,  24,  25,  26,  27,  28,  29,  30
#> NK: 31,  32,  33,  34,  35,  36,  37,  38,  39,  40
#> NK: 41,  42,  43,  44,  45,  46,  47,  48,  49,  50
#> NK: 51,  52,  53,  54,  55,  56,  57,  58,  59,  60
#> NK: 61,  62,  63,  64,  65,  66,  67,  68,  69,  70
#> NK: 71,  72,  73,  74,  75,  76,  77,  78,  79,  80
#> NK: 81,  82,  83,  84,  85,  86,  87,  88,  89,  90
#> NK: 91,  92,  93,  94,  95,  96,  97,  98,  99,  100
#> 
#> CV Q2 criterion:
#>   0   1 
#>   0 100 
#> 
#> CV Press criterion:
#>  1  2  3  4  5  6 
#> 14  0  0 22 20 44

The Q² criterion is recommended in that PLSR setting without missing data. A model with 1 component is selected by the cross-validation as displayed by the following figure. Hence the Q² criterion (1 component) does not agree with the experts (2 components).

plot(plsRglm::cvtable(summary(bbb2)),type="CVQ2")
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Component____ 4 ____
#> ____Component____ 5 ____
#> ____Component____ 6 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> 
#> NK: 1,  2,  3,  4,  5,  6,  7,  8,  9,  10
#> NK: 11,  12,  13,  14,  15,  16,  17,  18,  19,  20
#> NK: 21,  22,  23,  24,  25,  26,  27,  28,  29,  30
#> NK: 31,  32,  33,  34,  35,  36,  37,  38,  39,  40
#> NK: 41,  42,  43,  44,  45,  46,  47,  48,  49,  50
#> NK: 51,  52,  53,  54,  55,  56,  57,  58,  59,  60
#> NK: 61,  62,  63,  64,  65,  66,  67,  68,  69,  70
#> NK: 71,  72,  73,  74,  75,  76,  77,  78,  79,  80
#> NK: 81,  82,  83,  84,  85,  86,  87,  88,  89,  90
#> NK: 91,  92,  93,  94,  95,  96,  97,  98,  99,  100
#> 
#> CV Q2 criterion:
#>   0   1 
#>   0 100 
#> 
#> CV Press criterion:
#>  1  2  3  4  5  6 
#> 14  0  0 22 20 44

plot of chunk pineplotcvtableQ2

As for the CV Press criterion it is unable to point out a unique number of components.

plot(plsRglm::cvtable(summary(bbb2)),type="CVPress")
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Component____ 4 ____
#> ____Component____ 5 ____
#> ____Component____ 6 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> 
#> NK: 1,  2,  3,  4,  5,  6,  7,  8,  9,  10
#> NK: 11,  12,  13,  14,  15,  16,  17,  18,  19,  20
#> NK: 21,  22,  23,  24,  25,  26,  27,  28,  29,  30
#> NK: 31,  32,  33,  34,  35,  36,  37,  38,  39,  40
#> NK: 41,  42,  43,  44,  45,  46,  47,  48,  49,  50
#> NK: 51,  52,  53,  54,  55,  56,  57,  58,  59,  60
#> NK: 61,  62,  63,  64,  65,  66,  67,  68,  69,  70
#> NK: 71,  72,  73,  74,  75,  76,  77,  78,  79,  80
#> NK: 81,  82,  83,  84,  85,  86,  87,  88,  89,  90
#> NK: 91,  92,  93,  94,  95,  96,  97,  98,  99,  100
#> 
#> CV Q2 criterion:
#>   0   1 
#>   0 100 
#> 
#> CV Press criterion:
#>  1  2  3  4  5  6 
#> 14  0  0 22 20 44

plot of chunk pineplotcvtablePress

PLS (Y,T) Bootstrap

The package features our bootstrap based algorithm to select the number of components in plsR regression. It is implemented with the nbcomp.bootplsR function.

set.seed(4619)
nbcomp.bootplsR(Y=ypine,X=Xpine,R =500)
#> [1] 1
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> [1] 2
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> [1] 3
#> ____************************************************____
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Predicting X without NA neither in X nor in Y____
#> ****________________________________________________****
#> 
#> [1] "Optimal number of components: K = 2"
#> [1] 2

The verbose=FALSE option suppresses messages output during the algorithm, which is useful to replicate the bootstrap technique. To set up parallel computing, you can use the parallel and the ncpus options.

set.seed(4619)
res_boot_rep <- replicate(20,nbcomp.bootplsR(Y=ypine,X=Xpine,R =500,verbose =FALSE,parallel = "multicore",ncpus = 2))

It is easy to display the results with the barplot function.

barplot(table(res_boot_rep))

plot of chunk barplotresbootrep

A model with two components should be selected using our bootstrap based algorithm to select the number of components. Hence the number of component selected with our algorithm agrees with what was stated by the experts.

sPLS (Y,T) Bootstrap

The package also features our bootstrap based algorithm to select, for a given η value, the number of components in spls regression. It is implemented with the nbcomp.bootspls function.

nbcomp.bootspls(x=Xpine,y=ypine,eta=.5)
#> eta = 0.5 
#> [1] 1
#> [1] 2
#> [1] 3
#> [1] 4
#> 
#> Optimal parameters: eta = 0.5, K = 3

plot of chunk nbcompbootspls

#> $mspemat
#>                          
#> eta= 0.5 , K= 3 0.9595453
#> 
#> $eta.opt
#> [1] 0.5
#> 
#> $K.opt
#> [1] 3

A doParallel and foreach based parallel computing version of the algorithm is implemented as the nbcomp.bootspls.para function.

nbcomp.bootspls.para(x=Xpine,y=ypine,eta=.5)
#> [1] "eta = 0.5"
#> [1] 2
#> [1] 3
#> 
#> Optimal parameters: eta = 0.5, K = 2

plot of chunk spls

#> $mspemat
#>                         
#> eta= 0.5 ; K= 2 1.131643
#> 
#> $eta.opt
#> [1] 0.5
#> 
#> $K.opt
#> [1] 2
nbcomp.bootspls.para(x=Xpine,y=ypine,eta=c(.2,.5))
#> [1] "eta = 0.2"
#> [1] 2
#> [1] 3
#> [1] "eta = 0.5"
#> [1] 2
#> [1] 3
#> 
#> Optimal parameters: eta = 0.5, K = 2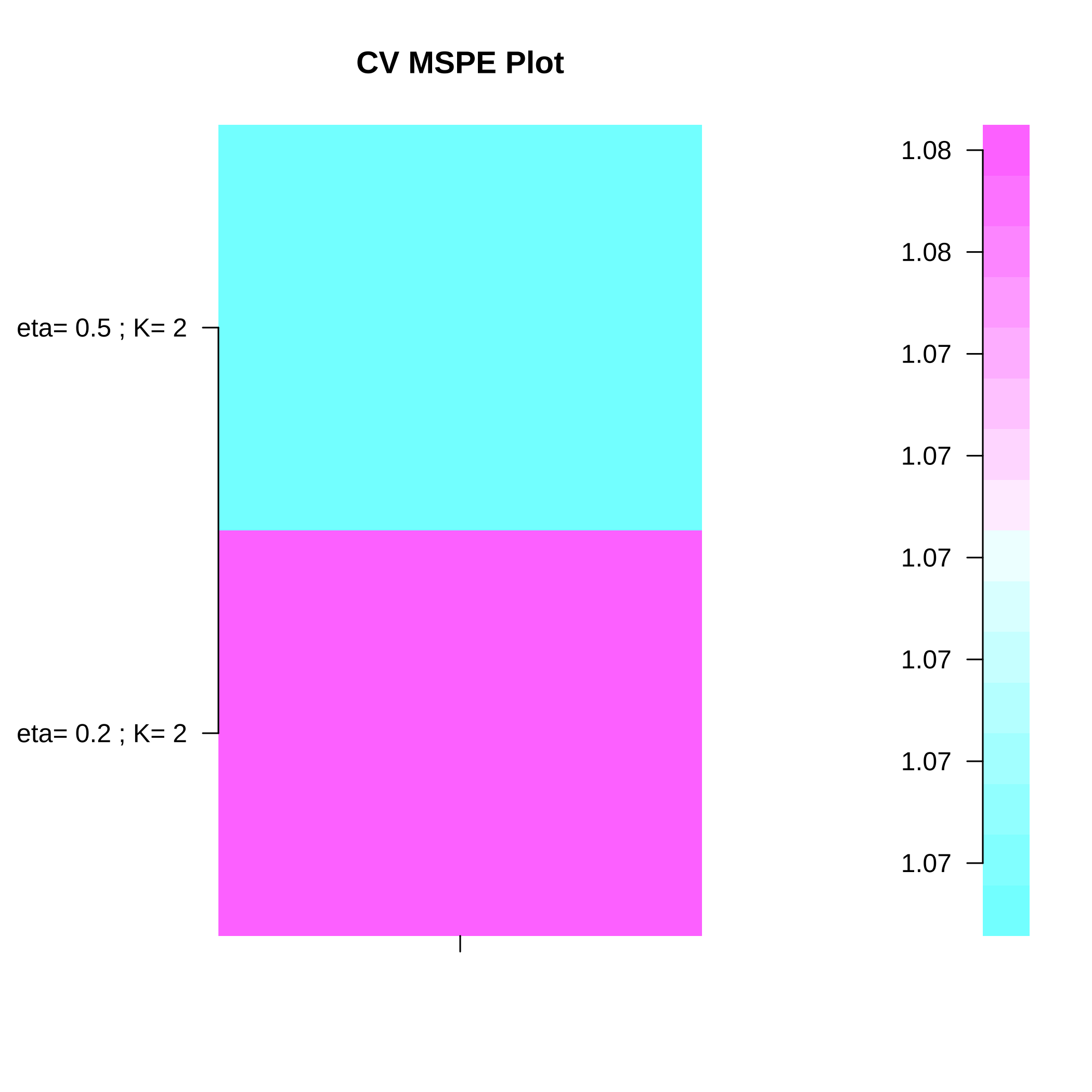

plot of chunk spls

#> $mspemat
#>                         
#> eta= 0.2 ; K= 2 1.076495
#> eta= 0.5 ; K= 2 1.067325
#> 
#> $eta.opt
#> [1] 0.5
#> 
#> $K.opt
#> result.2 
#>        2

Bootstrap (Y,X) for the coefficients with number of components updated for each resampling

Pinewood worm data reloaded.

library(bootPLS)
library(plsRglm)
data(pine, package = "plsRglm")
Xpine<-pine[,1:10]
ypine<-log(pine[,11])
datasetpine <- cbind(ypine,Xpine)

coefs.plsR.adapt.ncomp(datasetpine,sample(1:nrow(datasetpine)))
#>  [1]  2.000000000  8.064227044 -0.003019447
#>  [4] -0.054389603 -0.005212285 -0.109946405
#>  [7]  0.038799785 -0.078324545 -1.334080678
#> [10] -0.045021804 -0.390730689  0.054696227

Replicate the results to get the bootstrap distributions of the selected number of components and the coefficients.

replicate(20,coefs.plsR.adapt.ncomp(datasetpine,sample(1:nrow(datasetpine))))
#>               [,1]         [,2]         [,3]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>               [,4]         [,5]         [,6]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>               [,7]         [,8]         [,9]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>              [,10]        [,11]        [,12]
#>  [1,]  4.000000000  2.000000000  2.000000000
#>  [2,] 10.934323181  8.064227044  8.064227044
#>  [3,] -0.004164703 -0.003019447 -0.003019447
#>  [4,] -0.061586032 -0.054389603 -0.054389603
#>  [5,]  0.038677103 -0.005212285 -0.005212285
#>  [6,] -0.568792403 -0.109946405 -0.109946405
#>  [7,]  0.135567126  0.038799785  0.038799785
#>  [8,]  0.447111779 -0.078324545 -0.078324545
#>  [9,] -0.885736030 -1.334080678 -1.334080678
#> [10,] -0.110684199 -0.045021804 -0.045021804
#> [11,] -1.141903333 -0.390730689 -0.390730689
#> [12,] -0.397050615  0.054696227  0.054696227
#>              [,13]        [,14]        [,15]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>              [,16]        [,17]        [,18]
#>  [1,]  4.000000000  2.000000000  2.000000000
#>  [2,] 10.934323181  8.064227044  8.064227044
#>  [3,] -0.004164703 -0.003019447 -0.003019447
#>  [4,] -0.061586032 -0.054389603 -0.054389603
#>  [5,]  0.038677103 -0.005212285 -0.005212285
#>  [6,] -0.568792403 -0.109946405 -0.109946405
#>  [7,]  0.135567126  0.038799785  0.038799785
#>  [8,]  0.447111779 -0.078324545 -0.078324545
#>  [9,] -0.885736030 -1.334080678 -1.334080678
#> [10,] -0.110684199 -0.045021804 -0.045021804
#> [11,] -1.141903333 -0.390730689 -0.390730689
#> [12,] -0.397050615  0.054696227  0.054696227
#>              [,19]        [,20]
#>  [1,]  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227

Parallel computing support with the ncpus and parallel="multicore" options.

coefs.plsR.adapt.ncomp(datasetpine,sample(1:nrow(datasetpine)),ncpus=2,parallel="multicore")
#>  [1]  4.000000000 10.934323181 -0.004164703
#>  [4] -0.061586032  0.038677103 -0.568792403
#>  [7]  0.135567126  0.447111779 -0.885736030
#> [10] -0.110684199 -1.141903333 -0.397050615

replicate(20,coefs.plsR.adapt.ncomp(datasetpine,sample(1:nrow(datasetpine)),ncpus=2,parallel="multicore"))
#>               [,1]         [,2]         [,3]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>               [,4]         [,5]         [,6]
#>  [1,]  2.000000000  4.000000000  2.000000000
#>  [2,]  8.064227044 10.934323181  8.064227044
#>  [3,] -0.003019447 -0.004164703 -0.003019447
#>  [4,] -0.054389603 -0.061586032 -0.054389603
#>  [5,] -0.005212285  0.038677103 -0.005212285
#>  [6,] -0.109946405 -0.568792403 -0.109946405
#>  [7,]  0.038799785  0.135567126  0.038799785
#>  [8,] -0.078324545  0.447111779 -0.078324545
#>  [9,] -1.334080678 -0.885736030 -1.334080678
#> [10,] -0.045021804 -0.110684199 -0.045021804
#> [11,] -0.390730689 -1.141903333 -0.390730689
#> [12,]  0.054696227 -0.397050615  0.054696227
#>               [,7]         [,8]         [,9]
#>  [1,]  2.000000000  4.000000000  2.000000000
#>  [2,]  8.064227044 10.934323181  8.064227044
#>  [3,] -0.003019447 -0.004164703 -0.003019447
#>  [4,] -0.054389603 -0.061586032 -0.054389603
#>  [5,] -0.005212285  0.038677103 -0.005212285
#>  [6,] -0.109946405 -0.568792403 -0.109946405
#>  [7,]  0.038799785  0.135567126  0.038799785
#>  [8,] -0.078324545  0.447111779 -0.078324545
#>  [9,] -1.334080678 -0.885736030 -1.334080678
#> [10,] -0.045021804 -0.110684199 -0.045021804
#> [11,] -0.390730689 -1.141903333 -0.390730689
#> [12,]  0.054696227 -0.397050615  0.054696227
#>              [,10]        [,11]        [,12]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>              [,13]        [,14]        [,15]
#>  [1,]  4.000000000  2.000000000  2.000000000
#>  [2,] 10.934323181  8.064227044  8.064227044
#>  [3,] -0.004164703 -0.003019447 -0.003019447
#>  [4,] -0.061586032 -0.054389603 -0.054389603
#>  [5,]  0.038677103 -0.005212285 -0.005212285
#>  [6,] -0.568792403 -0.109946405 -0.109946405
#>  [7,]  0.135567126  0.038799785  0.038799785
#>  [8,]  0.447111779 -0.078324545 -0.078324545
#>  [9,] -0.885736030 -1.334080678 -1.334080678
#> [10,] -0.110684199 -0.045021804 -0.045021804
#> [11,] -1.141903333 -0.390730689 -0.390730689
#> [12,] -0.397050615  0.054696227  0.054696227
#>              [,16]        [,17]        [,18]
#>  [1,]  2.000000000  2.000000000  2.000000000
#>  [2,]  8.064227044  8.064227044  8.064227044
#>  [3,] -0.003019447 -0.003019447 -0.003019447
#>  [4,] -0.054389603 -0.054389603 -0.054389603
#>  [5,] -0.005212285 -0.005212285 -0.005212285
#>  [6,] -0.109946405 -0.109946405 -0.109946405
#>  [7,]  0.038799785  0.038799785  0.038799785
#>  [8,] -0.078324545 -0.078324545 -0.078324545
#>  [9,] -1.334080678 -1.334080678 -1.334080678
#> [10,] -0.045021804 -0.045021804 -0.045021804
#> [11,] -0.390730689 -0.390730689 -0.390730689
#> [12,]  0.054696227  0.054696227  0.054696227
#>              [,19]        [,20]
#>  [1,]  2.000000000  4.000000000
#>  [2,]  8.064227044 10.934323181
#>  [3,] -0.003019447 -0.004164703
#>  [4,] -0.054389603 -0.061586032
#>  [5,] -0.005212285  0.038677103
#>  [6,] -0.109946405 -0.568792403
#>  [7,]  0.038799785  0.135567126
#>  [8,] -0.078324545  0.447111779
#>  [9,] -1.334080678 -0.885736030
#> [10,] -0.045021804 -0.110684199
#> [11,] -0.390730689 -1.141903333
#> [12,]  0.054696227 -0.397050615

Aze real dataset: binary logistic plsRglm and sgpls regressions

PLSGLR (Y,T) Bootstrap

Loading the data and creating the data frames.

data(aze_compl)
Xaze_compl<-aze_compl[,2:34]
yaze_compl<-aze_compl$y
dataset <- cbind(y=yaze_compl,Xaze_compl)

Fitting a logistic PLS regression model with 10 components. You have to use the family option when fitting the plsRglm.

modplsglm <- plsRglm(y~.,data=dataset,10,modele="pls-glm-family",family="binomial")
#> ____************************************************____
#> 
#> Family: binomial 
#> Link function: logit 
#> 
#> ____Component____ 1 ____
#> ____Component____ 2 ____
#> ____Component____ 3 ____
#> ____Component____ 4 ____
#> ____Component____ 5 ____
#> ____Component____ 6 ____
#> ____Component____ 7 ____
#> ____Component____ 8 ____
#> ____Component____ 9 ____
#> ____Component____ 10 ____
#> ____Predicting X without NA neither in X or Y____
#> ****________________________________________________****

Perform the bootstrap based algorithm with the nbcomp.bootplsRglm function. By default 250 resamplings are carried out.

set.seed(4619)
aze_compl.bootYT <- suppressWarnings(nbcomp.bootplsRglm(modplsglm))

Plotting the bootstrap distributions of the coefficients of the components.

plsRglm::boxplots.bootpls(aze_compl.bootYT)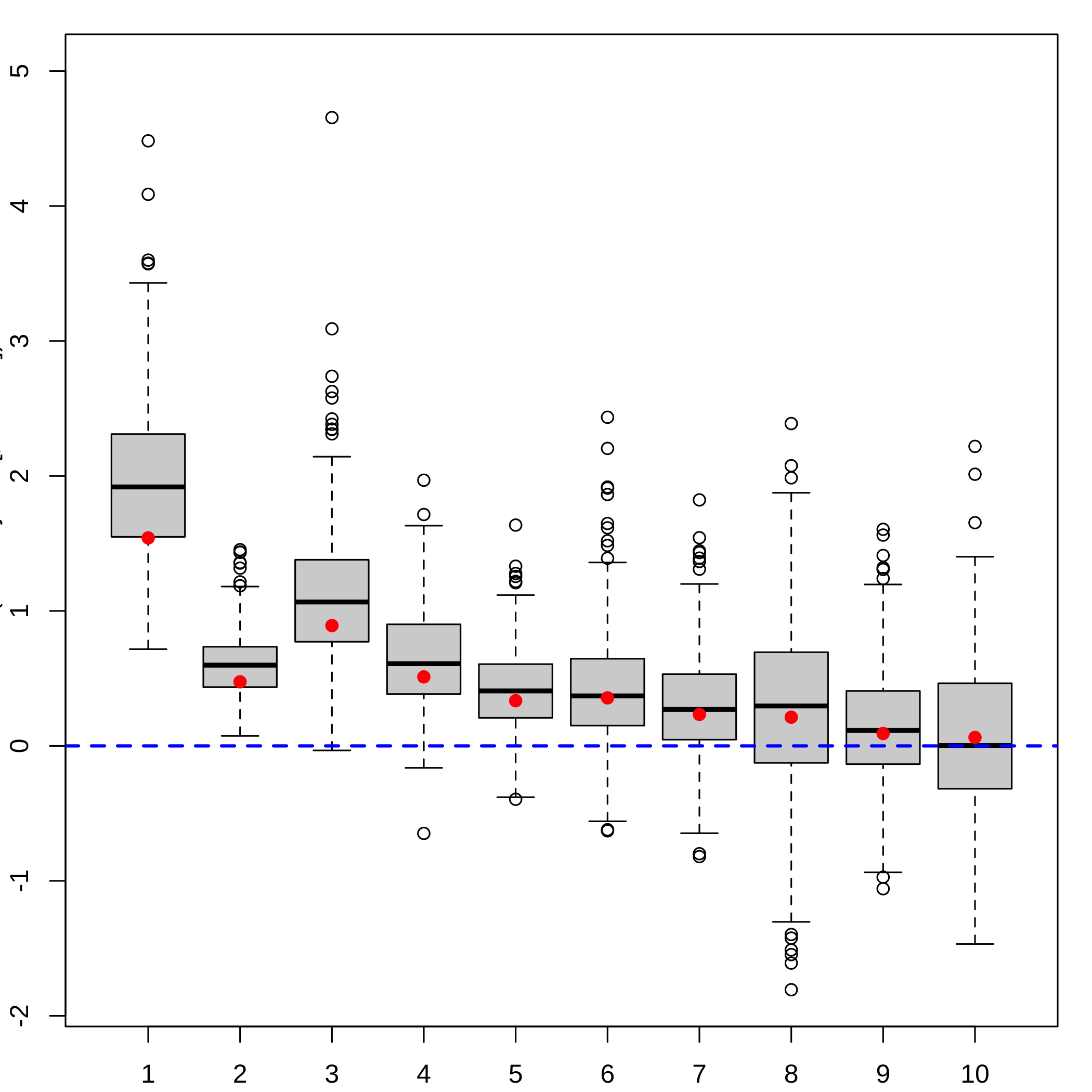

plot of chunk azeplotbootcomp

Computing the bootstrap based confidence intervals of the coefficients of the components.

plsRglm::confints.bootpls(aze_compl.bootYT)
#> Warning in norm.inter(t, adj.alpha): extreme
#> order statistics used as endpoints

#> Warning in norm.inter(t, adj.alpha): extreme
#> order statistics used as endpoints

#> Warning in norm.inter(t, adj.alpha): extreme
#> order statistics used as endpoints
#>                                                
#>  [1,] -0.1909709 2.3581748 -0.4489036 1.9697388
#>  [2,] -0.1514302 0.8243332 -0.3376837 0.7471037
#>  [3,] -0.4319055 1.7434199 -0.6285256 1.5594694
#>  [4,] -0.3748813 1.0973698 -0.5490521 0.9657205
#>  [5,] -0.3963722 0.8830876 -0.5130832 0.8905919
#>  [6,] -0.6441165 1.2480090 -0.9267788 1.1913771
#>  [7,] -0.6863159 1.0264625 -0.8829492 1.0706084
#>  [8,] -1.1970167 1.4738770 -1.2043483 1.7957092
#>  [9,] -0.8340372 0.9057530 -1.0433636 0.9124285
#> [10,] -1.0786394 1.2056122 -1.1600493 1.2398892
#>                                       
#>  [1,]  1.11236461 3.531007  0.71686088
#>  [2,]  0.20267973 1.287467  0.07412900
#>  [3,]  0.22338048 2.411375 -0.03355241
#>  [4,]  0.05733105 1.572104 -0.45493576
#>  [5,] -0.22108731 1.182588 -0.38904916
#>  [6,] -0.47946992 1.638686 -0.53350462
#>  [7,] -0.60361567 1.349942 -0.75368847
#>  [8,] -1.37023450 1.629823 -1.54876392
#>  [9,] -0.72858196 1.227210 -0.74456869
#> [10,] -1.11385399 1.286084 -1.02902293
#>                
#>  [1,] 2.1861124
#>  [2,] 0.8286440
#>  [3,] 1.6424348
#>  [4,] 1.1619803
#>  [5,] 0.9004701
#>  [6,] 1.4582694
#>  [7,] 1.0112706
#>  [8,] 1.3140140
#>  [9,] 1.1516065
#> [10,] 1.3514701
#> attr(,"typeBCa")
#> [1] TRUE

Computing the bootstrap based confidence intervals of the coefficients of the components.

suppressWarnings(plsRglm::plots.confints.bootpls(plsRglm::confints.bootpls(aze_compl.bootYT)))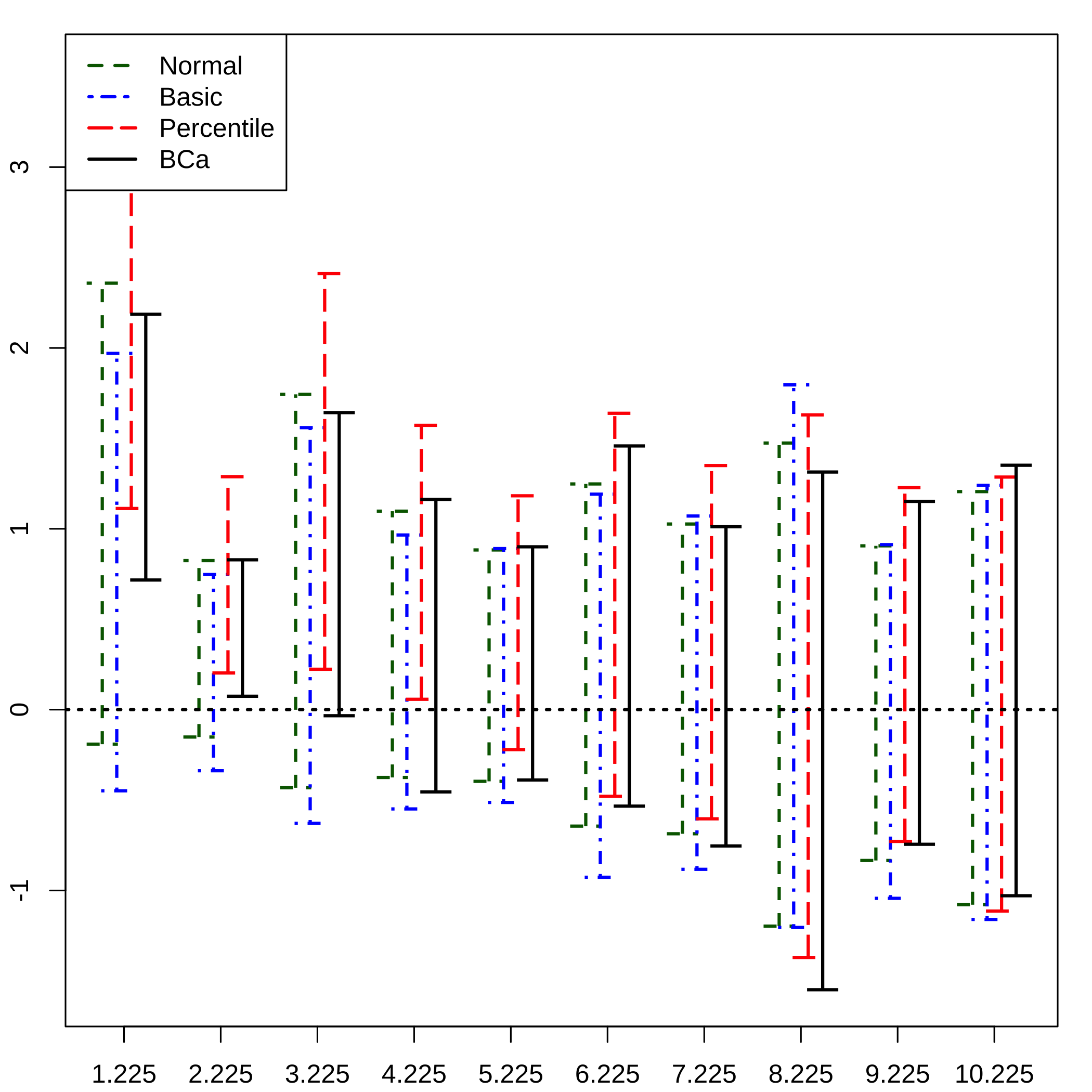

plot of chunk azebootcompplotCI

sparse PLSGLR (Y,T) Bootstrap

The package also features our bootstrap based algorithm to select, for a given η value, the number of components in sgpls regression. It is implemented in the nbcomp.bootsgpls.

set.seed(4619)
data(prostate, package="spls")
nbcomp.bootsgpls((prostate$x)[,1:30], prostate$y, R=250, eta=0.2, typeBCa = FALSE)
#> [1] "eta = 0.2"
#> [1] "K = 1"
#> [1] "K = 2"
#> [1] "K = 3"
#> [1] "K = 4"
#> [1] "K = 5"
#> Warning: glm.fit: fitted probabilities
#> numerically 0 or 1 occurred
#> 
#> Optimal parameters: eta = 0.2, K = 4

plot of chunk prostateload

#> $err.mat
#>                          
#> eta= 0.2 ; K= 4 0.2554545
#> 
#> $eta.opt
#> [1] 0.2
#> 
#> $K.opt
#> [1] 4
#> 
#> $cands
#>           [,1] [,2] [,3] [,4]
#> [1,] 0.2554545   30  0.2    4

A doParallel and foreach based parallel computing version of the algorithm is implemented as the nbcomp.bootspls.para function.

nbcomp.bootsgpls.para((prostate$x)[,1:30], prostate$y, R=250, eta=c(.2,.5), maxnt=10, typeBCa = FALSE)
#> [1] "eta = 0.2"
#> [1] "K = 1"
#> [1] "K = 2"
#> [1] "K = 3"
#> [1] "K = 4"
#> [1] "K = 5"
#> [1] "eta = 0.5"
#> [1] "K = 1"
#> [1] "K = 2"
#> [1] "K = 3"
#> [1] "K = 4"
#> [1] "K = 5"
#> Warning: glm.fit: algorithm did not converge
#> Warning: glm.fit: fitted probabilities
#> numerically 0 or 1 occurred

#> Warning: glm.fit: fitted probabilities
#> numerically 0 or 1 occurred

#> Warning: glm.fit: fitted probabilities
#> numerically 0 or 1 occurred
#> 
#> Optimal parameters: eta = 0.5, K = 4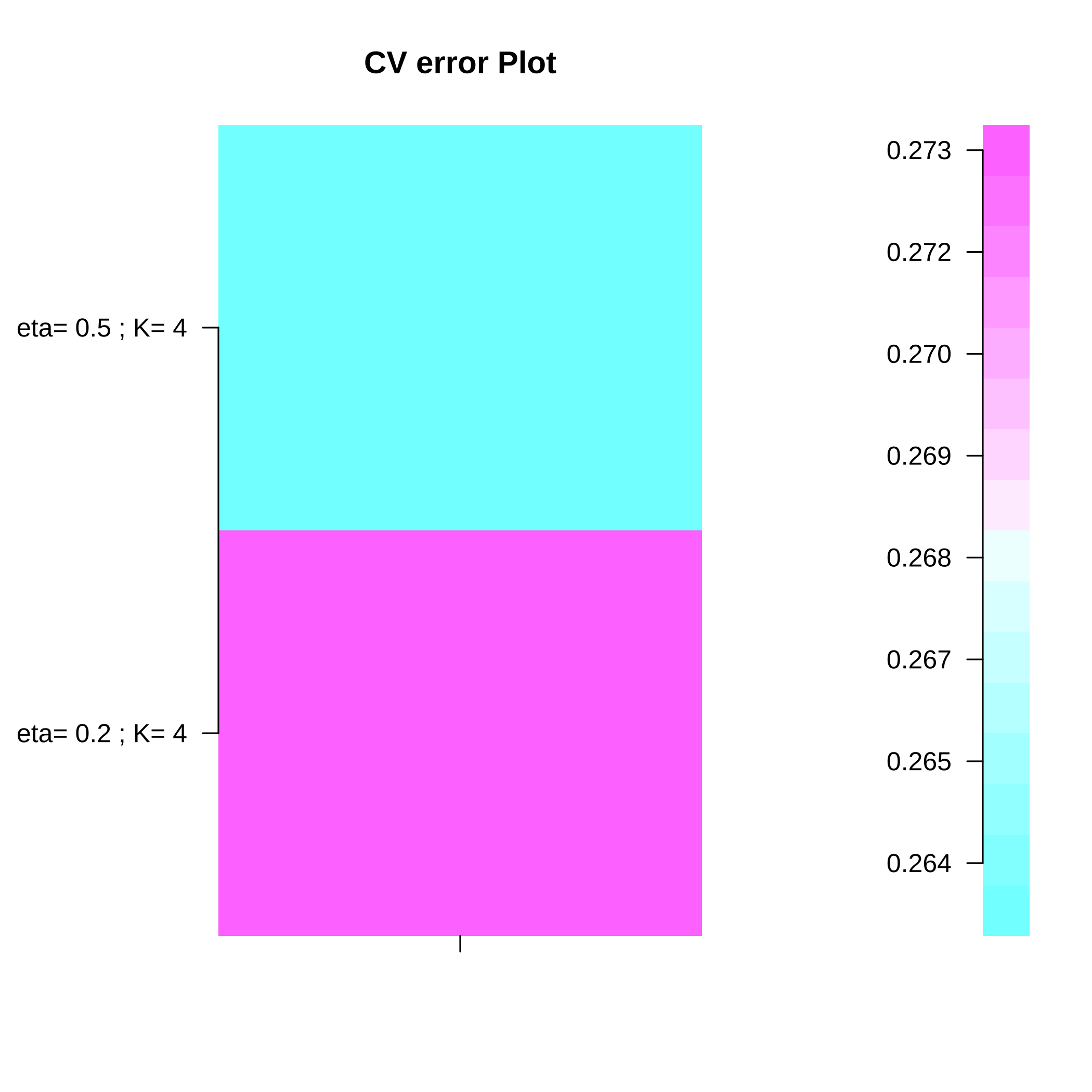

plot of chunk prostatespls

#> $err.mat
#>                          
#> eta= 0.2 ; K= 4 0.2727273
#> eta= 0.5 ; K= 4 0.2636364
#> 
#> $eta.opt
#> [1] 0.5
#> 
#> $K.opt
#> [1] 4
#> 
#> $cands
#>           [,1] [,2] [,3] [,4]
#> [1,] 0.2636364 27.4  0.5    4

rm(list=c("Xpine","ypine","bbb","bbb2","aze_compl","Xaze_compl","yaze_compl","aze_compl.bootYT","dataset","modplsglm","pine","datasetpine","prostate","res_boot_rep"))