Getting started with bigPLScox

Introduction

The bigPLScox package provides tools to fit Partial Least Squares (PLS) models tailored to the Cox proportional hazards setting. It includes cross-validation helpers, diagnostic utilities, and interfaces that work with both in-memory matrices and bigmemory objects. This vignette walks through a core workflow on the allelotyping dataset bundled with the package.

Loading the data

library(bigPLScox)

data(micro.censure)
data(Xmicro.censure_compl_imp)

Y_all <- micro.censure$survyear[1:80]
status_all <- micro.censure$DC[1:80]
X_all <- apply(
  as.matrix(Xmicro.censure_compl_imp),
  MARGIN = 2,
  FUN = as.numeric
)[1:80, ]

set.seed(2024)
train_id <- 1:60
test_id <- 61:80

X_train <- X_all[train_id, ]
X_test <- X_all[test_id, ]
Y_train <- Y_all[train_id]
Y_test <- Y_all[test_id]
status_train <- status_all[train_id]
status_test <- status_all[test_id]

The original factor-based design matrix is also available should you prefer to work with categorical predictors directly.

X_train_raw <- Xmicro.censure_compl_imp[train_id, ]
X_test_raw <- Xmicro.censure_compl_imp[test_id, ]

Exploring deviance residuals

computeDR() extracts deviance residuals from a null Cox model. Inspecting them before fitting the PLS components helps detect anomalies in the survival outcomes.

residuals_overview <- computeDR(Y_train, status_train, plot = TRUE)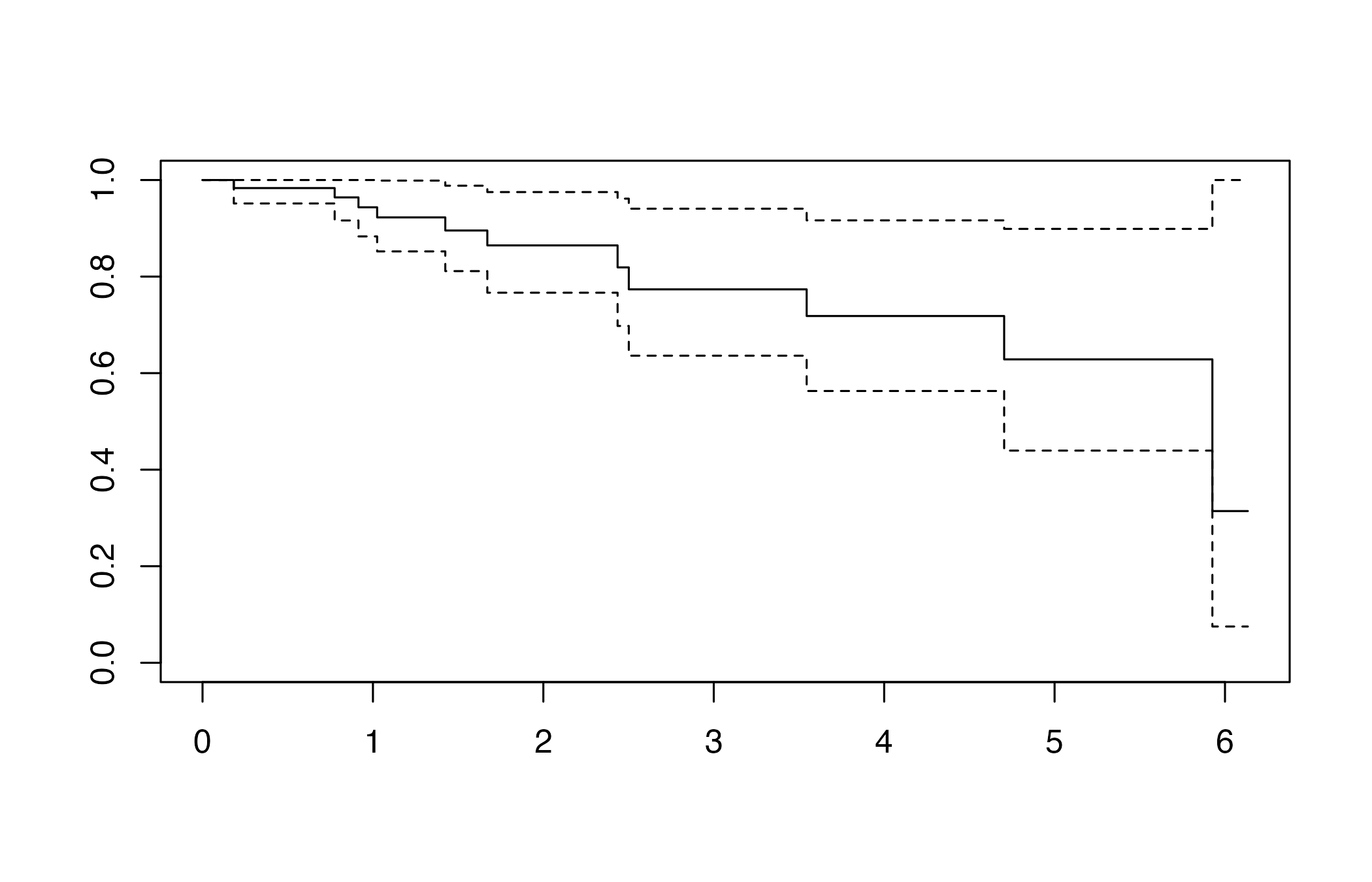

eta_null <- rep(0, length(Y_train))
head(residuals_overview)
#>          1          2          3          4          5          6 
#> -1.3771591 -0.5360370 -0.2693493 -0.3994329 -0.8040940 -0.3994329

if (requireNamespace("bench", quietly = TRUE)) {
  benchmark_dr <- bench::mark(
    survival = computeDR(Y_train, status_train, engine = "survival"),
    cpp = computeDR(Y_train, status_train, engine = "cpp", eta = eta_null),
    iterations = 10,
    check = FALSE
  )
  benchmark_dr
}
#> # A tibble: 2 × 6
#>   expression      min   median `itr/sec` mem_alloc `gc/sec`
#>   <bch:expr> <bch:tm> <bch:tm>     <dbl> <bch:byt>    <dbl>
#> 1 survival    819.8µs  849.3µs     1128.     175KB        0
#> 2 cpp          85.5µs   98.1µs     9055.     159KB        0

all.equal(
  as.numeric(computeDR(Y_train, status_train, engine = "survival")),
  as.numeric(computeDR(Y_train, status_train, engine = "cpp", eta = eta_null)),
  tolerance = 1e-7
)
#> [1] TRUE

Fitting Cox PLS models

The matrix interface to coxgpls() mirrors survival::coxph() while adding latent components that stabilise estimation in high dimensions.

set.seed(123)
cox_pls_fit <- coxgpls(
  Xplan = X_train,
  time = Y_train,
  status = status_train,
  ncomp = 6,
    ind.block.x = c(3, 10, 20)
)
cox_pls_fit
#> Call:
#> coxph(formula = YCsurv ~ ., data = tt_gpls)
#> 
#>          coef exp(coef) se(coef)      z        p
#> dim.1 -0.7368    0.4786   0.1162 -6.340  2.3e-10
#> dim.2 -0.5256    0.5912   0.1382 -3.804 0.000142
#> dim.3 -0.3314    0.7179   0.1199 -2.763 0.005720
#> dim.4 -0.2883    0.7495   0.1092 -2.641 0.008272
#> dim.5 -0.4002    0.6702   0.1435 -2.788 0.005298
#> dim.6 -0.2696    0.7636   0.1239 -2.176 0.029529
#> 
#> Likelihood ratio test=60.94  on 6 df, p=2.906e-11
#> n= 60, number of events= 60

A formula interface is also available when working with data frames that include both predictors and survival outcomes.

cox_pls_fit_formula <- coxgpls(
  ~ ., Y_train, status_train,
  ncomp = 6,
  ind.block.x = c(3, 10, 20),
  dataXplan = data.frame(X_train_raw)
)
cox_pls_fit_formula
#> Call:
#> coxph(formula = YCsurv ~ ., data = tt_gpls)
#> 
#>           coef exp(coef) se(coef)      z       p
#> dim.1 -0.82612   0.43775  0.31903 -2.589 0.00961
#> dim.2 -0.79075   0.45350  0.39461 -2.004 0.04508
#> dim.3 -0.89888   0.40703  0.30294 -2.967 0.00301
#> dim.4  0.02354   1.02382  0.29663  0.079 0.93675
#> dim.5 -0.40714   0.66555  0.40456 -1.006 0.31423
#> dim.6 -0.53689   0.58456  0.38554 -1.393 0.16374
#> 
#> Likelihood ratio test=19.59  on 6 df, p=0.00328
#> n= 60, number of events= 11

Cross-validation utilities

Repeated cross-validation helps determine the appropriate number of latent components. Provide either a matrix or a list with x, time, and status entries.

set.seed(123456)
cv_results <- suppressWarnings(cv.coxgpls(
  list(x = X_train, time = Y_train, status = status_train),
  nt = 6,
  ind.block.x = c(3, 10, 20)
))
#> CV Fold 1 
#> CV Fold 2 
#> CV Fold 3 
#> CV Fold 4 
#> CV Fold 5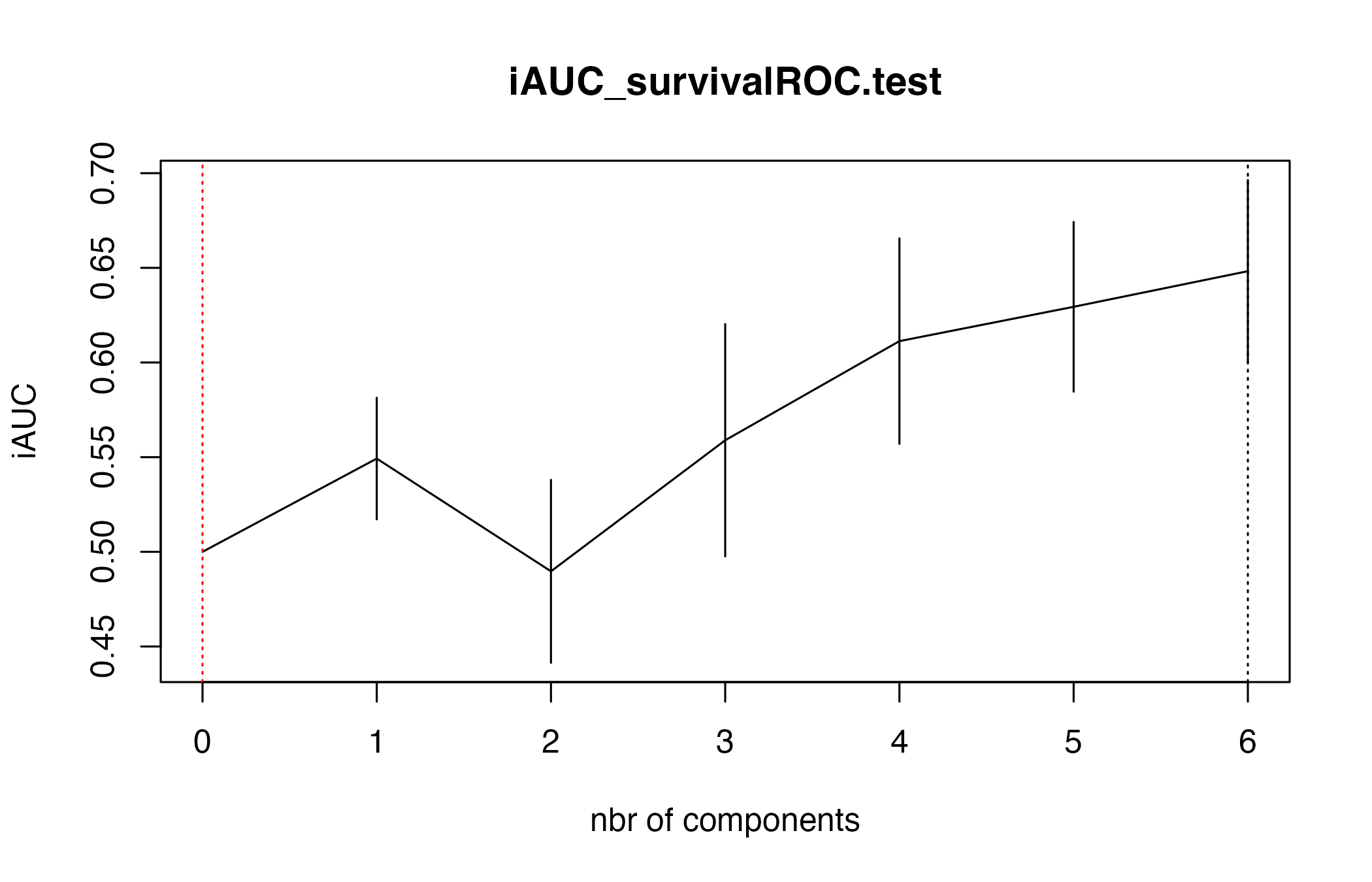

cv_results
#> $nt
#> [1] 6
#> 
#> $cv.error10
#> [1] 0.5000000 0.5492633 0.4897065 0.5589258 0.6112917 0.6294183 0.6482323
#> 
#> $cv.se10
#> [1] 0.00000000 0.03211886 0.04830433 0.06137605 0.05429528 0.04481718 0.04814978
#> 
#> $folds
#> $folds$`1`
#>  [1] 60 45  3 57 21 15 35 22 51 12 20 13
#> 
#> $folds$`2`
#>  [1] 42 54 50 28  1 41  6 18 44  8 27 25
#> 
#> $folds$`3`
#>  [1] 59 36 55 52 24 46 37 19  4 47 33  5
#> 
#> $folds$`4`
#>  [1] 49 38 30  2 34 48 53 31 11 56 26 39
#> 
#> $folds$`5`
#>  [1]  7 10 23 16 14 58 29  9 43 17 40 32
#> 
#> 
#> $lambda.min10
#> [1] 6
#> 
#> $lambda.1se10
#> [1] 0

The selected number of components is stored under cv_results$opt_nt. Use it to refit the model with the deviance residual solver for comparison.

set.seed(123456)
cox_pls_dr <- coxgplsDR(
  Xplan = X_train,
  time = Y_train,
  status = status_train,
  ncomp = cv_results$nt,
  ind.block.x = c(3, 10, 20)
)
cox_pls_dr
#> Call:
#> coxph(formula = YCsurv ~ ., data = tt_gplsDR)
#> 
#>         coef exp(coef) se(coef)     z        p
#> dim.1 0.7329    2.0812   0.1120 6.545 5.95e-11
#> dim.2 0.6418    1.8999   0.1456 4.409 1.04e-05
#> dim.3 0.3467    1.4144   0.1080 3.210  0.00133
#> dim.4 0.4266    1.5320   0.1554 2.745  0.00605
#> dim.5 0.3694    1.4468   0.1453 2.542  0.01101
#> dim.6 0.2884    1.3343   0.1095 2.633  0.00847
#> 
#> Likelihood ratio test=63.84  on 6 df, p=7.442e-12
#> n= 60, number of events= 60

DK-splines extension

For flexible baseline hazards the coxDKgplsDR() estimator augments the PLS components with DK-splines. The interface mirrors the previous functions.

cox_DKsplsDR_fit <- coxDKgplsDR(
  Xplan = X_train,
  time = Y_train,
  status = status_train,
  ncomp = 6,
  validation = "CV",
  ind.block.x = c(3, 10, 20),
  verbose = FALSE
)
cox_DKsplsDR_fit
#> Call:
#> coxph(formula = YCsurv ~ ., data = tt_DKgplsDR)
#> 
#>           coef exp(coef) se(coef)     z        p
#> dim.1   4.8792  131.5255   0.7348 6.640 3.14e-11
#> dim.2   4.3106   74.4853   0.8523 5.058 4.25e-07
#> dim.3   4.3799   79.8304   1.0374 4.222 2.42e-05
#> dim.4   3.1313   22.9036   0.9043 3.463 0.000535
#> dim.5   1.9561    7.0716   0.7031 2.782 0.005400
#> dim.6   1.9467    7.0054   0.7344 2.651 0.008031
#> 
#> Likelihood ratio test=77.54  on 6 df, p=1.151e-14
#> n= 60, number of events= 60

Cross-validation is available for the DK-splines estimator as well.

set.seed(2468)
cv_coxDKgplsDR_res <- suppressWarnings(cv.coxDKgplsDR(
  list(x = X_train, time = Y_train, status = status_train),
  nt = 6,
  ind.block.x = c(3, 10, 20)
))
#> Kernel :  rbfdot 
#> Estimated_sigma  0.01258323 
#> CV Fold 1 
#> Kernel :  rbfdot 
#> Estimated_sigma  0.01471071 
#> CV Fold 2 
#> Kernel :  rbfdot 
#> Estimated_sigma  0.0127949 
#> CV Fold 3 
#> Kernel :  rbfdot 
#> Estimated_sigma  0.0122611 
#> CV Fold 4 
#> Kernel :  rbfdot 
#> Estimated_sigma  0.01289496 
#> CV Fold 5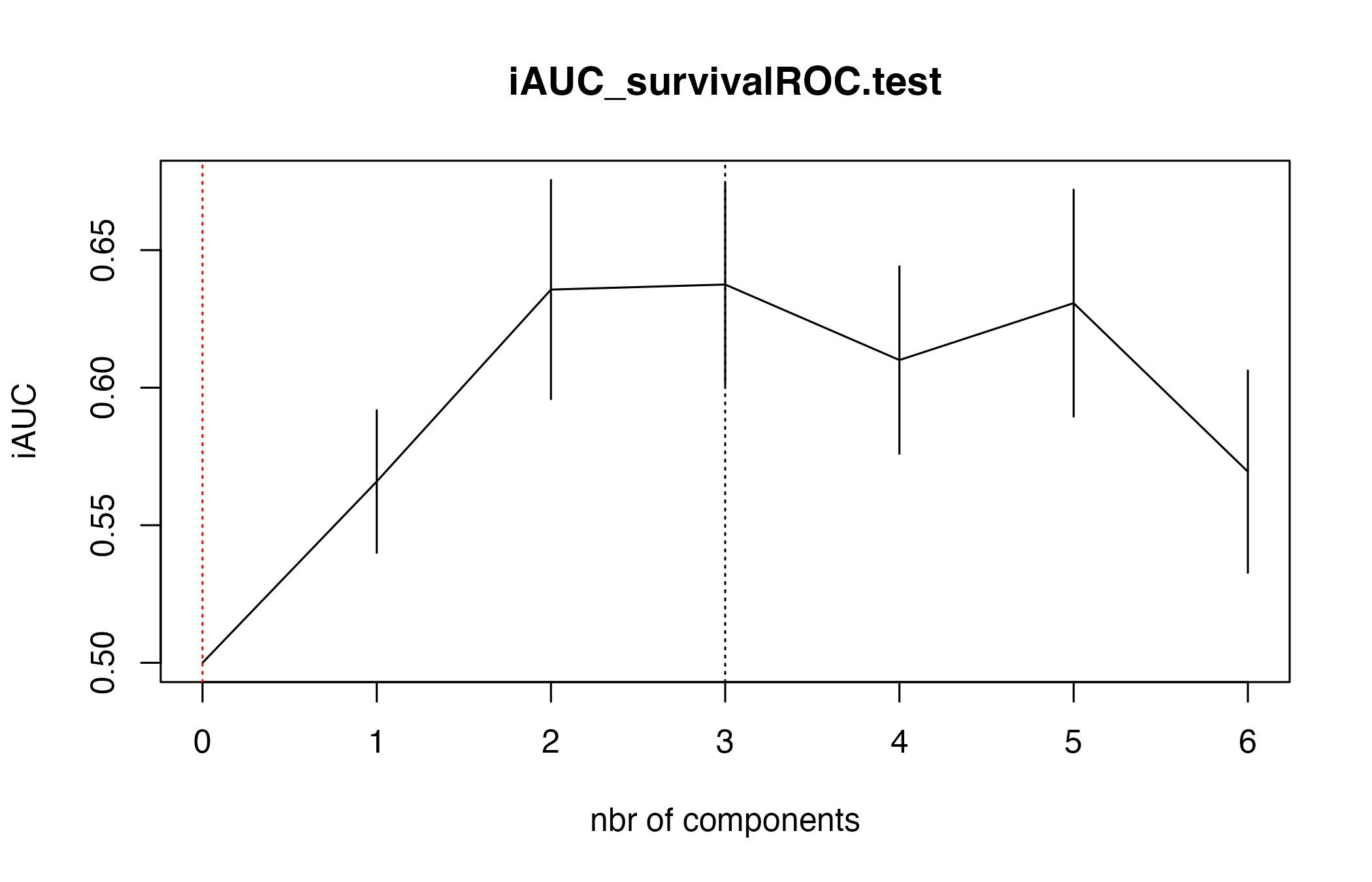

cv_coxDKgplsDR_res
#> $nt
#> [1] 6
#> 
#> $cv.error10
#> [1] 0.5000000 0.5658906 0.6356608 0.6374963 0.6100371 0.6307320 0.5694802
#> 
#> $cv.se10
#> [1] 0.00000000 0.02591444 0.03982352 0.03646931 0.03407857 0.04124367 0.03676530
#> 
#> $folds
#> $folds$`1`
#>  [1] 44 16 27 26 55 20 49 14  6 47 18  7
#> 
#> $folds$`2`
#>  [1] 58  8  2 17  3 15 52 43 56 11 29 59
#> 
#> $folds$`3`
#>  [1] 51 13 57 46 45 32 19  5 36 33 10 28
#> 
#> $folds$`4`
#>  [1] 21 50 38 60 53 42 23 31 12 24  1 25
#> 
#> $folds$`5`
#>  [1] 22 39 35 54  4 30 34 48 37 40  9 41
#> 
#> 
#> $lambda.min10
#> [1] 3
#> 
#> $lambda.1se10
#> [1] 0

# Unified prediction comparison

if (requireNamespace("bigmemory", quietly = TRUE)) {
  library(bigmemory)
  X_big_train <- bigmemory::as.big.matrix(X_train)
  X_big_test <- bigmemory::as.big.matrix(X_test)
  big_fit <- big_pls_cox(X_big_train, Y_train, status_train, ncomp = 4)
  gd_fit <- big_pls_cox_gd(X_big_train, Y_train, status_train, ncomp = 4, max_iter = 200)

  risk_table <- data.frame(
    subject = seq_along(test_id),
    big_pls = predict(big_fit, newdata = X_big_test, type = "link", comps = 1:4),
    big_pls_gd = predict(gd_fit, newdata = X_big_test, type = "link", comps = 1:4)
  )

  if (requireNamespace("plsRcox", quietly = TRUE)) {
    pls_fit <- try(plsRcox::plsRcox(Y_train, status_train, X_train_raw, nt = 4), silent = TRUE)
    if (!inherits(pls_fit, "try-error") && !is.null(pls_fit$Coefficients)) {
      risk_table$plsRcox <- as.numeric(as.matrix(X_test_raw) %*% pls_fit$Coefficients)
    }
  }

  risk_table

  apply(
    risk_table[-1],
    2,
    function(lp) {
      survival::concordance(survival::Surv(Y_test, status_test) ~ lp)$concordance
    }
  )
}
#> ____************************************************____
#>    big_pls big_pls_gd 
#>  0.3023256  0.3023256

Next steps

vignette("bigPLScox-overview", package = "bigPLScox") summarises the main modelling functions and their big-memory counterparts.
vignette("bigPLScox-benchmarking", package = "bigPLScox") explains how to reproduce performance comparisons with the scripts under inst/benchmarks/.
The README and package website provide further references and data preparation tips for large-scale studies.

Frédéric Bertrand