Chapitre 04. Analyse en composantes principales (ACP).

Description des données

Échantillon de 50 villes (individus) tirées aléatoirement sur la pollution de l’air aux États-Unis en 1960

TMR : taux de mortalité exprimé en 1/10000
GE65 : pourcentage (multiplié par 10) de la population des 65 ans et plus
LPOP : logarithme (en base 10 et multiplié par 10) de la population
NONPOOR : pourcentage de ménages avec un revenu au dessus du seuil de pauvreté
PERWH : pourcentage de population blanche
PMEAN : moyenne arithmétique des relevés réalisés deux fois par semaine de particules suspendues dans l’air (micro-g/m3 multiplié par 10)
PMIN : plus petite valeur des relevés réalisés deux fois par semaine de particules suspendues dans l’air (micro-g/m3 multiplié par 10)
LPMAX : logarithme de la plus grande valeur des relevés réalisés deux fois par semaine de particules suspendues dans l’air (micro-g/m3 multiplié par 10)
SMEAN : moyenne arithmétique des relevés réalisés deux fois par semaine de sulfate (micro-g/m3 multiplié par 10)
SMIN : plus petite valeur des relevés réalisés deux fois par semaine de sulfate (micro-g/m3 multiplié par 10)
SMAX : plus grande valeur des relevés réalisés deux fois par semaine de sulfate (micro-g/m3 multiplié par 10)
LPM2 : logarithme de la densité de la population par mile carré (multiplié par 0,1)

Lecture des données

library(sageR)
data(air_pollution)

Élimine les variables PM2 et PMAX qui sont transformées en logarithme dans les variables l_pm2 et l_pmax.

air_pollution <- air_pollution[,-(8:9)]

Quelques statistiques descriptives du fichier de données

summary(air_pollution)
#>        CITY         TMR              SMIN            SMEAN       
#>  JACKSON : 2   Min.   : 618.0   Min.   :  1.00   Min.   : 27.00  
#>  AUGUSTA : 1   1st Qu.: 806.5   1st Qu.: 27.25   1st Qu.: 62.25  
#>  AUSTIN  : 1   Median : 882.5   Median : 43.50   Median : 79.50  
#>  BEAUMONT: 1   Mean   : 893.9   Mean   : 47.36   Mean   : 98.18  
#>  BOSTON  : 1   3rd Qu.: 955.2   3rd Qu.: 62.00   3rd Qu.:132.50  
#>  BRIDGEPO: 1   Max.   :1199.0   Max.   :155.00   Max.   :283.00  
#>  (Other) :43                                                     
#>       SMAX            PMIN           PMEAN            PERWH      
#>  Min.   : 58.0   Min.   :10.00   Min.   : 54.00   Min.   :60.00  
#>  1st Qu.:139.5   1st Qu.:29.75   1st Qu.: 90.25   1st Qu.:83.03  
#>  Median :194.5   Median :46.00   Median :121.00   Median :90.65  
#>  Mean   :220.0   Mean   :46.86   Mean   :122.48   Mean   :87.50  
#>  3rd Qu.:265.2   3rd Qu.:57.50   3rd Qu.:147.00   3rd Qu.:95.08  
#>  Max.   :940.0   Max.   :98.00   Max.   :247.00   Max.   :99.30  
#>                                                                  
#>     NONPOOR           GE65             LPOP           l_pm2      
#>  Min.   :67.80   Min.   : 45.00   Min.   :4.937   Min.   :1.808  
#>  1st Qu.:76.58   1st Qu.: 70.25   1st Qu.:5.384   1st Qu.:3.251  
#>  Median :82.65   Median : 81.50   Median :5.570   Median :3.637  
#>  Mean   :81.57   Mean   : 81.32   Mean   :5.639   Mean   :3.814  
#>  3rd Qu.:87.10   3rd Qu.: 93.75   3rd Qu.:5.831   3rd Qu.:4.398  
#>  Max.   :90.70   Max.   :116.00   Max.   :6.794   Max.   :7.213  
#>                                                                  
#>      l_pmax     
#>  Min.   :4.820  
#>  1st Qu.:5.247  
#>  Median :5.489  
#>  Mean   :5.521  
#>  3rd Qu.:5.777  
#>  Max.   :6.865  
#>

Exercice 4.1 : Analyse visuelle des données

Standardisation des données.

air_pollution_std <- scale(air_pollution[,-1])

Affichage graphique du tableau de données sans la variable CITY qui est en première colonne.

z <- t(as.matrix(air_pollution_std))
x <- seq(1,12,length.out=12)
y <- seq(1,50,length.out=50)
rownames(z) <- c("TMR","SMIN","SMEAN","SMAX","PMIN","PMEAN","PERWH","NONPOOR","GE65","LPOP","l_pm2","l_pmax")
colnames(z) <- air_pollution$CITY
image(x,y,z,xlab="Variables",ylab="Villes",main="Représentation des données standardisées -  Air Pollution",axes=FALSE)
axis(1, at = x,labels = rownames(z),las=1,cex.axis=1)
axis(2, at = y,labels = colnames(z),las=2,cex.axis=0.4)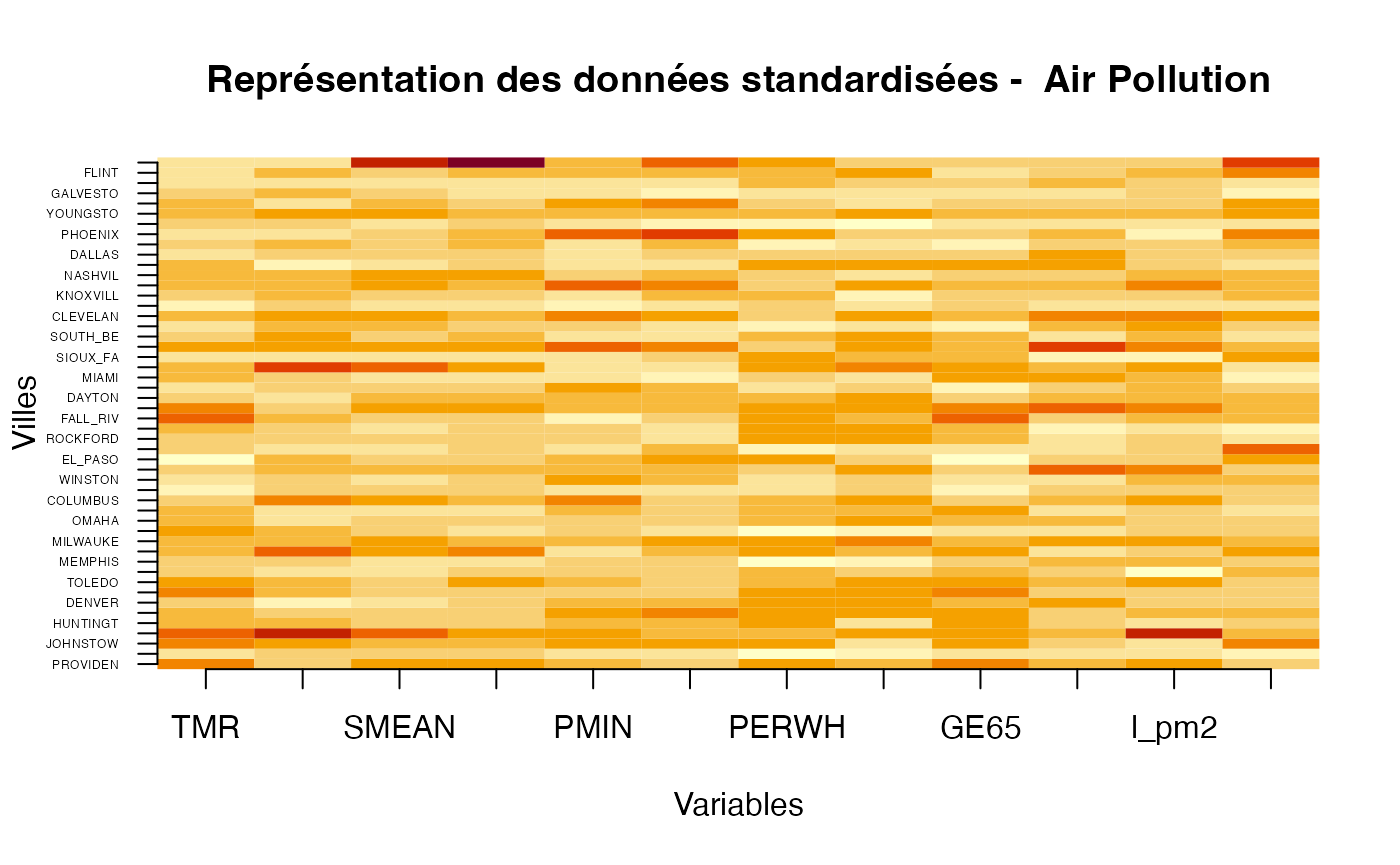

Exercice 4.2 : Analyse des corrélations entre les variables

GGally::ggpairs(air_pollution[,-1], progress=FALSE)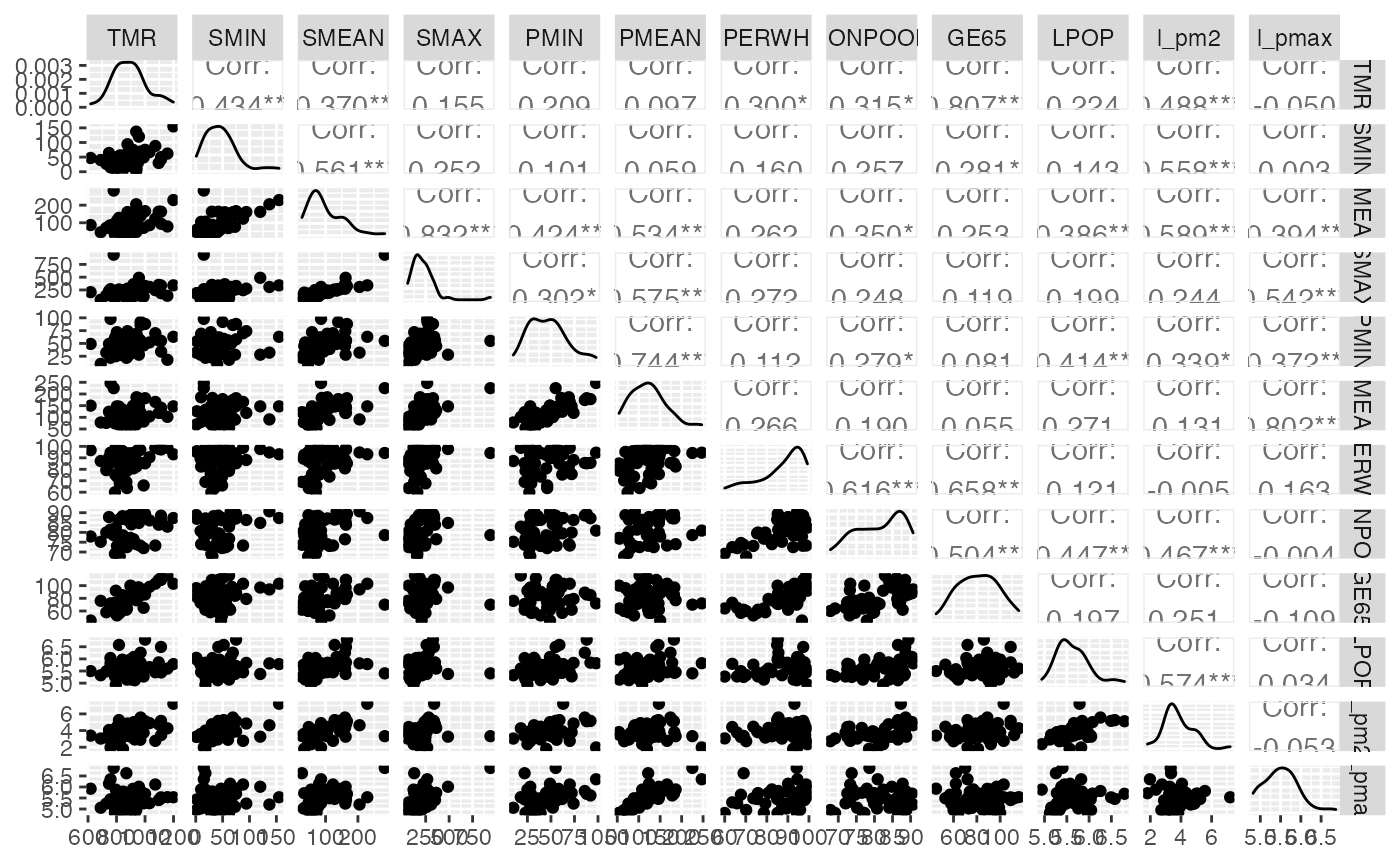
#> Registered S3 method overwritten by 'GGally':
#>   method from   
#>   +.gg   ggplot2

cor_pollution <- cor(air_pollution[,-1])
col1 <- colorRampPalette(c("#7F0000", "red", "#FF7F00", "yellow", "white", "cyan", "#007FFF", "blue", "#00007F"))
col2 <- colorRampPalette(c("#67001F", "#B2182B", "#D6604D", "#F4A582", "#FDDBC7", "#FFFFFF", "#D1E5F0", "#92C5DE", "#4393C3", "#2166AC", "#053061"))
col3 <- colorRampPalette(c("red", "white", "blue")) 
col4 <- colorRampPalette(c("#7F0000", "red", "#FF7F00", "yellow", "#7FFF7F", "cyan", "#007FFF", "blue", "#00007F"))
whiteblack <- c("white", "black")
corrplot::corrplot(cor_pollution, method = "color", addrect = 2, col = col1(100))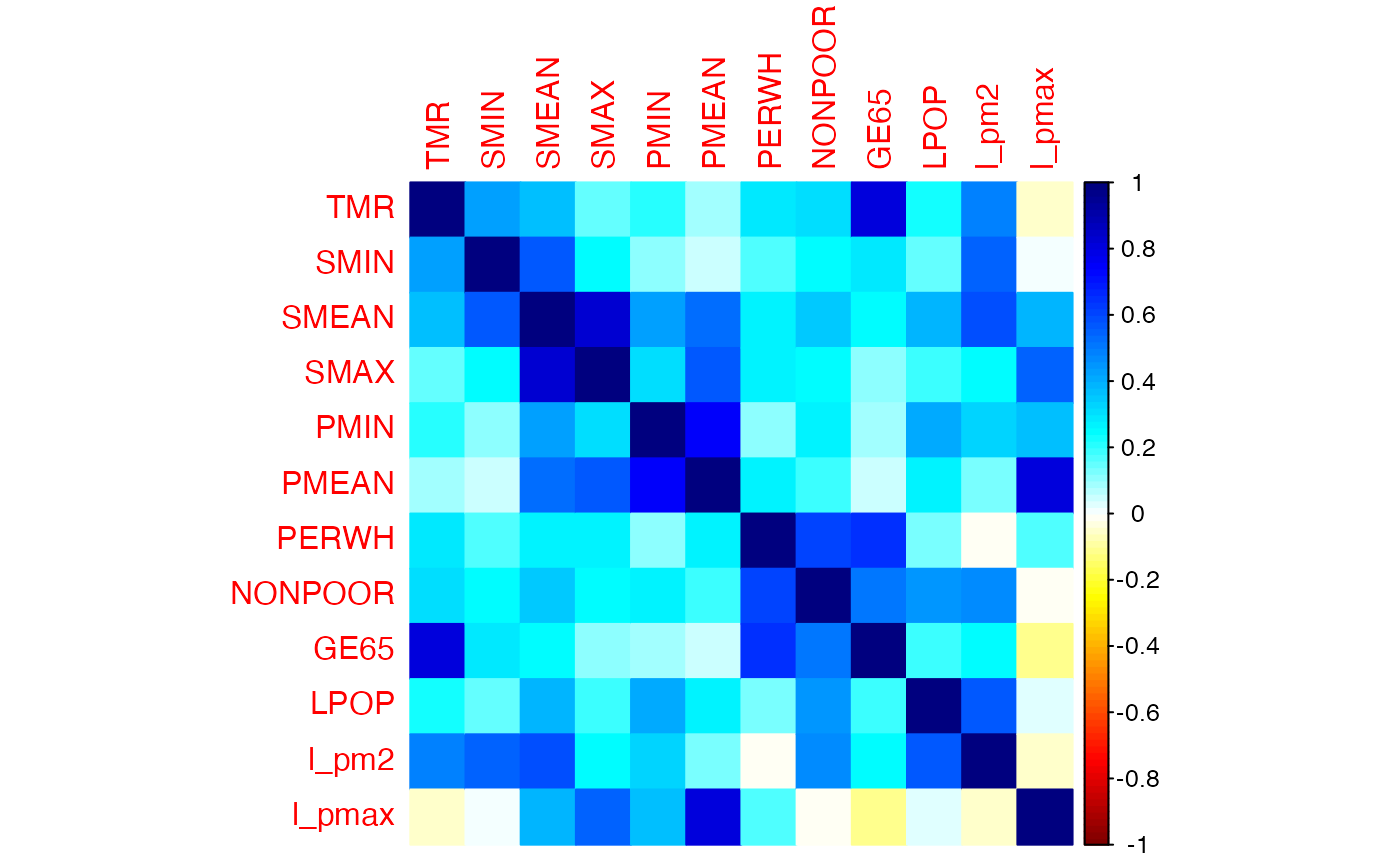

Exercice 4.3 : Analyse des inerties expliquées et résiduelles

library(FactoMineR)
res.PCA <- PCA(air_pollution[,-(1:2)])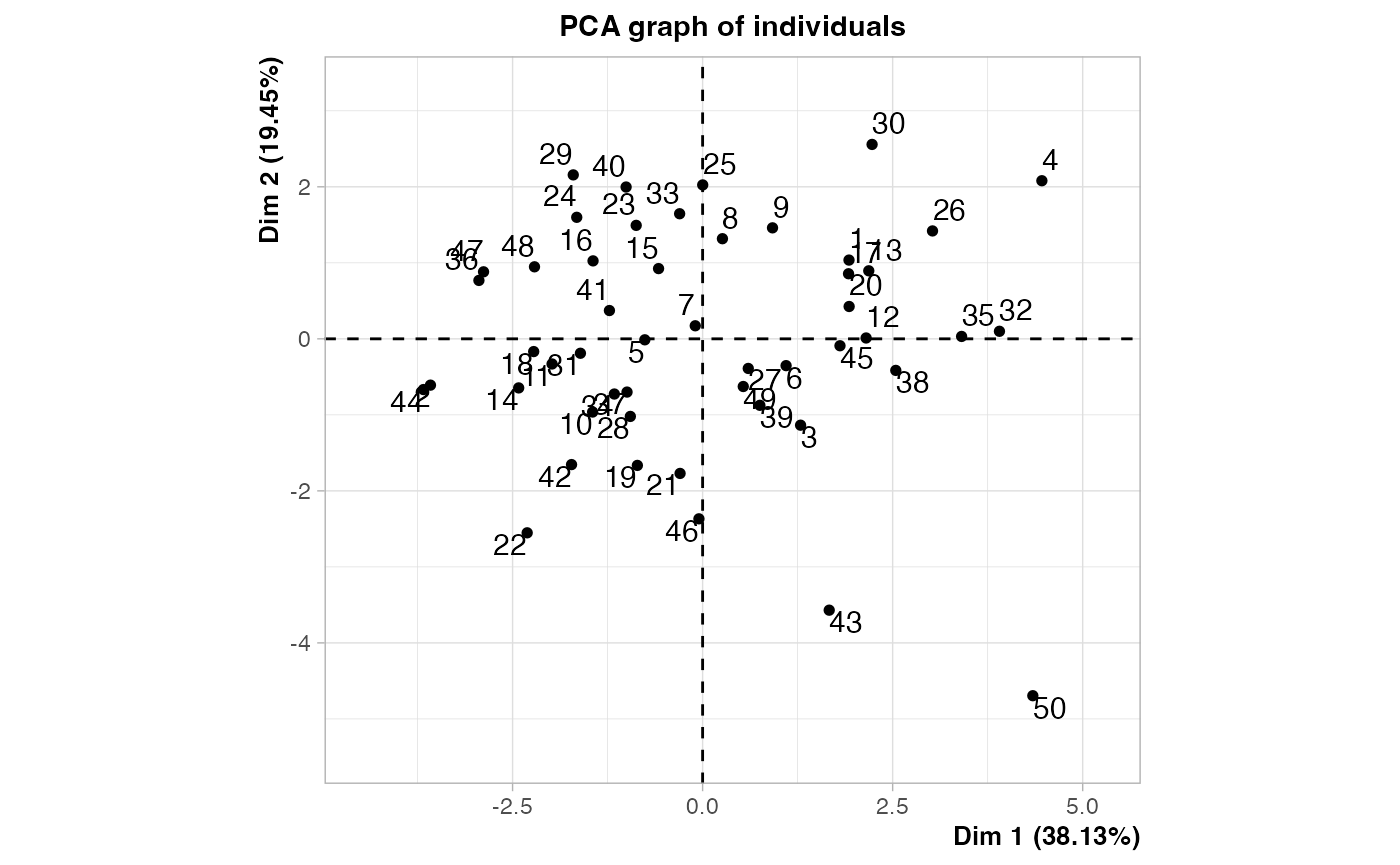

summary(res.PCA)
#> 
#> Call:
#> PCA(X = air_pollution[, -(1:2)]) 
#> 
#> 
#> Eigenvalues
#>                        Dim.1   Dim.2   Dim.3   Dim.4   Dim.5   Dim.6   Dim.7
#> Variance               4.194   2.139   1.509   1.159   0.629   0.433   0.386
#> % of var.             38.128  19.448  13.715  10.532   5.718   3.933   3.508
#> Cumulative % of var.  38.128  57.576  71.292  81.823  87.542  91.475  94.983
#>                        Dim.8   Dim.9  Dim.10  Dim.11
#> Variance               0.287   0.144   0.064   0.057
#> % of var.              2.606   1.310   0.586   0.516
#> Cumulative % of var.  97.589  98.898  99.484 100.000
#> 
#> Individuals (the 10 first)
#>             Dist    Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr
#> 1       |  2.847 |  1.926  1.768  0.458 |  1.036  1.003  0.132 |  0.569  0.430
#> 2       |  4.398 | -3.580  6.113  0.663 | -0.609  0.347  0.019 | -1.863  4.601
#> 3       |  3.483 |  1.289  0.792  0.137 | -1.136  1.206  0.106 |  1.368  2.481
#> 4       |  5.875 |  4.463  9.499  0.577 |  2.080  4.044  0.125 | -2.075  5.709
#> 5       |  2.344 | -0.760  0.276  0.105 | -0.013  0.000  0.000 |  1.041  1.435
#> 6       |  2.458 |  1.098  0.575  0.200 | -0.353  0.116  0.021 |  1.566  3.251
#> 7       |  2.296 | -0.097  0.004  0.002 |  0.172  0.028  0.006 |  1.163  1.793
#> 8       |  2.422 |  0.261  0.032  0.012 |  1.317  1.622  0.296 |  1.796  4.274
#> 9       |  2.073 |  0.920  0.403  0.197 |  1.460  1.993  0.496 | -0.137  0.025
#> 10      |  2.702 | -1.447  0.999  0.287 | -0.963  0.867  0.127 |  1.748  4.052
#>           cos2  
#> 1        0.040 |
#> 2        0.179 |
#> 3        0.154 |
#> 4        0.125 |
#> 5        0.197 |
#> 6        0.406 |
#> 7        0.257 |
#> 8        0.549 |
#> 9        0.004 |
#> 10       0.419 |
#> 
#> Variables (the 10 first)
#>            Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr   cos2  
#> SMIN    |  0.489  5.694  0.239 |  0.363  6.159  0.132 | -0.334  7.387  0.111 |
#> SMEAN   |  0.865 17.836  0.748 | -0.065  0.196  0.004 | -0.212  2.968  0.045 |
#> SMAX    |  0.725 12.545  0.526 | -0.324  4.911  0.105 |  0.040  0.107  0.002 |
#> PMIN    |  0.644  9.888  0.415 | -0.310  4.493  0.096 | -0.117  0.913  0.014 |
#> PMEAN   |  0.716 12.225  0.513 | -0.601 16.865  0.361 |  0.155  1.599  0.024 |
#> PERWH   |  0.494  5.813  0.244 |  0.321  4.824  0.103 |  0.746 36.855  0.556 |
#> NONPOOR |  0.621  9.195  0.386 |  0.504 11.878  0.254 |  0.239  3.793  0.057 |
#> GE65    |  0.434  4.481  0.188 |  0.594 16.484  0.353 |  0.461 14.092  0.213 |
#> LPOP    |  0.564  7.578  0.318 |  0.223  2.333  0.050 | -0.325  7.008  0.106 |
#> l_pm2   |  0.615  9.015  0.378 |  0.396  7.331  0.157 | -0.580 22.270  0.336 |

Exercice 4.4 : Contributions et reconstitutions des variables sur la première composante principale

res.PCA 
#> **Results for the Principal Component Analysis (PCA)**
#> The analysis was performed on 50 individuals, described by 11 variables
#> *The results are available in the following objects:
#> 
#>    name               description                          
#> 1  "$eig"             "eigenvalues"                        
#> 2  "$var"             "results for the variables"          
#> 3  "$var$coord"       "coord. for the variables"           
#> 4  "$var$cor"         "correlations variables - dimensions"
#> 5  "$var$cos2"        "cos2 for the variables"             
#> 6  "$var$contrib"     "contributions of the variables"     
#> 7  "$ind"             "results for the individuals"        
#> 8  "$ind$coord"       "coord. for the individuals"         
#> 9  "$ind$cos2"        "cos2 for the individuals"           
#> 10 "$ind$contrib"     "contributions of the individuals"   
#> 11 "$call"            "summary statistics"                 
#> 12 "$call$centre"     "mean of the variables"              
#> 13 "$call$ecart.type" "standard error of the variables"    
#> 14 "$call$row.w"      "weights for the individuals"        
#> 15 "$call$col.w"      "weights for the variables"

fournit la liste des informations disponibles.

name description
“$eig” “eigenvalues”
“$var” “results for the variables”
“$var$coord” “coord. for the variables”
“$var$cor” “correlations variables - dimensions”
“$var$cos2” “cos2 for the variables”
“$var$contrib” “contributions of the variables”
“$ind” “results for the individuals”
“$ind$coord” “coord. for the individuals”
“$ind$cos2” “cos2 for the individuals”
“$ind$contrib” “contributions of the individuals”
“$call” “summary statistics”
“$call$centre” “mean of the variables”
“$call$ecart.type” “standard error of the variables”
“$call$row.w” “weights for the individuals”
“$call$col.w” “weights for the variables”

contrib_dim_1 <- round(res.PCA$var$contrib[,1],2)
cos2_dim_1 <- round(res.PCA$var$cos2[,1]*100,2)
contrib_cos2_var_dim_1 <- data.frame(contrib_dim_1,cos2_dim_1)
contrib_cos2_var_dim_1
#>         contrib_dim_1 cos2_dim_1
#> SMIN             5.69      23.88
#> SMEAN           17.84      74.81
#> SMAX            12.54      52.61
#> PMIN             9.89      41.47
#> PMEAN           12.23      51.27
#> PERWH            5.81      24.38
#> NONPOOR          9.20      38.57
#> GE65             4.48      18.79
#> LPOP             7.58      31.78
#> l_pm2            9.01      37.81
#> l_pmax           5.73      24.03

Exercice 4.5 : Équation de la première composante principale

res.PCA$var$coord[,1]
#>      SMIN     SMEAN      SMAX      PMIN     PMEAN     PERWH   NONPOOR      GE65 
#> 0.4886781 0.8649000 0.7253509 0.6439964 0.7160517 0.4937540 0.6210111 0.4335012 
#>      LPOP     l_pm2    l_pmax 
#> 0.5637713 0.6148864 0.4902501

Exercice 4.6 : Contributions et reconstitutions des individus sur la première composante principale

CITY <- air_pollution$CITY
contrib_dim_1 <- round(res.PCA$ind$contrib[,1],2)
cos2_dim_1 <- round(res.PCA$ind$cos2[,1]*100,2)
contrib_cos2_ind_dim_1 <- data.frame(CITY,contrib_dim_1,cos2_dim_1)
contrib_cos2_ind_dim_1
#>        CITY contrib_dim_1 cos2_dim_1
#> 1  PROVIDEN          1.77      45.75
#> 2   JACKSON          6.11      66.26
#> 3  JOHNSTOW          0.79      13.69
#> 4  JERSEY_C          9.50      57.71
#> 5  HUNTINGT          0.28      10.52
#> 6  DES_MOIN          0.57      19.96
#> 7    DENVER          0.00       0.18
#> 8   READING          0.03       1.16
#> 9    TOLEDO          0.40      19.68
#> 10   FRESNO          1.00      28.67
#> 11  MEMPHIS          1.87      35.49
#> 12     YORK          2.21      29.03
#> 13 MILWAUKE          2.28      69.49
#> 14 SAVANNAH          2.79      54.48
#> 15    OMAHA          0.16      10.36
#> 16   TOPEKA          0.99      26.13
#> 17 COLUMBUS          1.76      46.47
#> 18 BEAUMONT          2.35      76.59
#> 19  WINSTON          0.35      10.28
#> 20  DETROIT          1.77      34.98
#> 21  EL_PASO          0.04       1.18
#> 22    MACON          2.54      29.45
#> 23 ROCKFORD          0.36      13.29
#> 24  JACKSON          1.31      30.36
#> 25 FALL_RIV          0.00       0.00
#> 26   BOSTON          4.36      62.60
#> 27   DAYTON          0.17      13.41
#> 28 CHARLOTT          0.43      18.39
#> 29    MIAMI          1.38      28.68
#> 30 BRIDGEPO          2.37      27.38
#> 31 SIOUX_FA          1.23      22.45
#> 32  CHICAGO          7.27      67.69
#> 33 SOUTH_BE          0.04       1.69
#> 34  NORFOLK          0.64      16.92
#> 35 CLEVELAN          5.54      75.80
#> 36   AUSTIN          4.13      82.38
#> 37 KNOXVILL          0.47      22.04
#> 38 INDIANAP          3.08      59.90
#> 39  NASHVIL          0.27      13.83
#> 40  SEATTLE          0.48       9.08
#> 41   DALLAS          0.72      32.85
#> 42   MOBILE          1.42      33.65
#> 43  PHOENIX          1.32      11.12
#> 44  AUGUSTA          6.43      79.60
#> 45 YOUNGSTO          1.56      77.36
#> 46 CHATTANO          0.00       0.03
#> 47 GALVESTO          3.96      68.37
#> 48 FORT_WOR          2.33      62.38
#> 49    FLINT          0.14       5.91
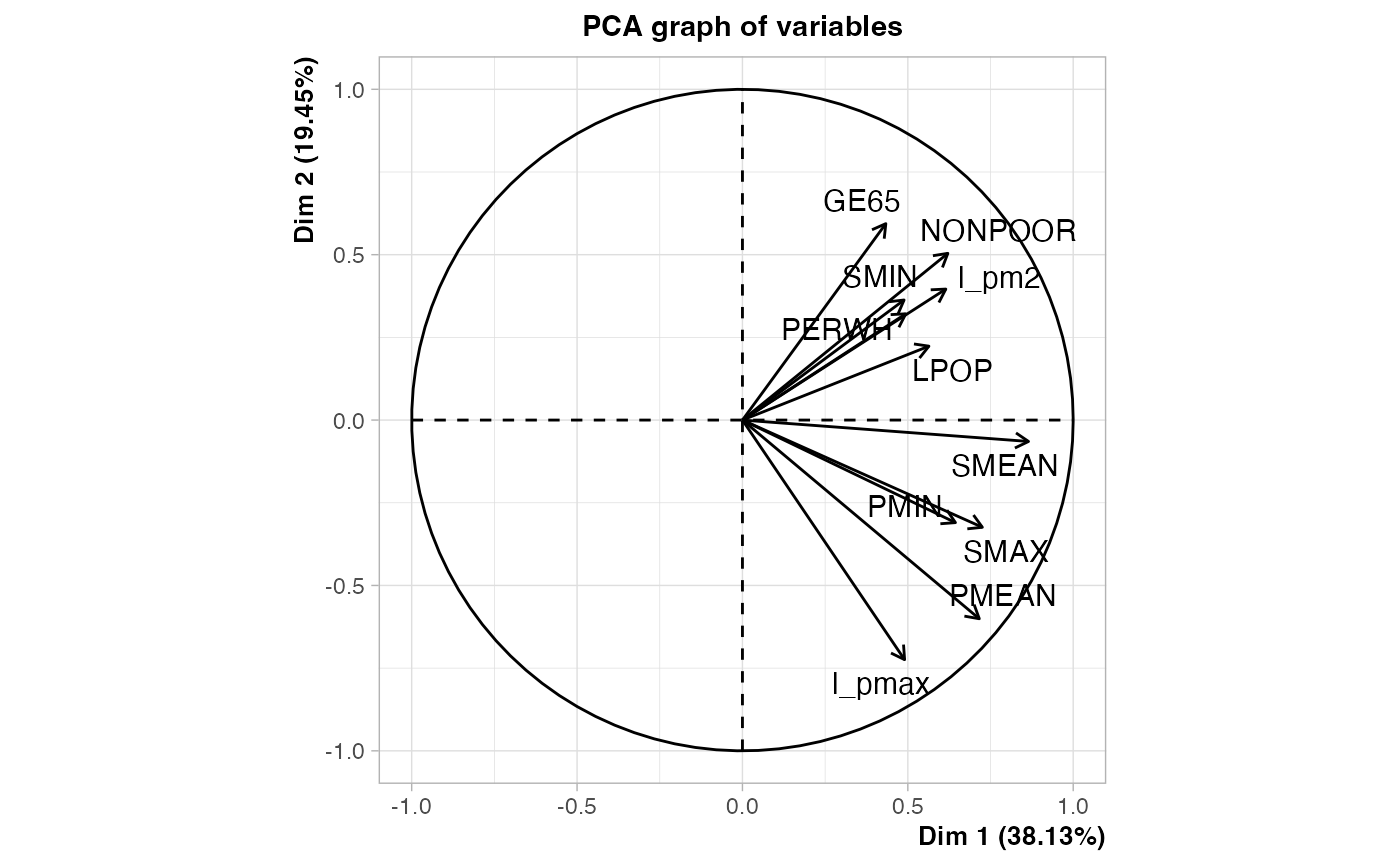
#> 50 CHARLEST          9.00      32.58

Exercice 4.7 : Cercle des corrélations

Le cercle des corrélations se situe dans la fenêtre graphique.

Exercice 4.8 : Analyse de la deuxième dimension

contrib_dim_2 <- round(res.PCA$var$contrib[,2],2)
cos2_dim_2 <- round(res.PCA$var$cos2[,2]*100,2)
contrib_cos2_var_dim_2 <- data.frame(contrib_dim_2,cos2_dim_2)
contrib_cos2_var_dim_2
#>         contrib_dim_2 cos2_dim_2
#> SMIN             6.16      13.18
#> SMEAN            0.20       0.42
#> SMAX             4.91      10.51
#> PMIN             4.49       9.61
#> PMEAN           16.87      36.08
#> PERWH            4.82      10.32
#> NONPOOR         11.88      25.41
#> GE65            16.48      35.26
#> LPOP             2.33       4.99
#> l_pm2            7.33      15.68
#> l_pmax          24.53      52.47

Tout le code avec R.

Christian Derquenne

2022-09-21