Chapitre 07. Classification automatique.

Exercice 7.2 : Construire la matrice de dissimilarités mixtes entre les 1000 champignons

Description des données : caractéristiques de champignons

num_champ : numéro du champignon
couleur_chapeau : couleur du chapeau
contusions : contusions
odeur : odeur du champignon
espacement_lamelle : espacement des lamelles
habitat : habitat

Lecture des données

library(sageR)
data(champignons)

Sélection des variables de l’étude

champ_sel <- champignons[, c("couleur_chapeau","contusions","odeur","espacement_lamelle","habitat")]

Transformation de la table en modalités codées

n=nrow(champ_sel)
m=18
DJ <- matrix(0,nrow=n,ncol=m)
for (i in 1:n)
    {if (champ_sel$espacement_lamelle[i] == "ferme") {DJ[i,1]=1}
     if (champ_sel$espacement_lamelle[i] == "serre") {DJ[i,2]=1}
     if (champ_sel$couleur_chapeau[i] == "blanc") {DJ[i,3]=1}
     if (champ_sel$couleur_chapeau[i] == "gris") {DJ[i,4]=1}
     if (champ_sel$couleur_chapeau[i] == "jaune") {DJ[i,5]=1}
     if (champ_sel$couleur_chapeau[i] == "marron") {DJ[i,6]=1}
     if (champ_sel$couleur_chapeau[i] == "rouge") {DJ[i,7]=1}
     if (champ_sel$contusions[i] == "abime") {DJ[i,8]=1}
     if (champ_sel$contusions[i] == "non") {DJ[i,9]=1}
     if (champ_sel$odeur[i] == "amande") {DJ[i,10]=1}
     if (champ_sel$odeur[i] == "anis") {DJ[i,11]=1}
     if (champ_sel$odeur[i] == "apre") {DJ[i,12]=1}
     if (champ_sel$odeur[i] == "inodore") {DJ[i,13]=1}
     if (champ_sel$habitat[i] == "foret") {DJ[i,14]=1}
     if (champ_sel$habitat[i] == "pelouse") {DJ[i,15]=1}
     if (champ_sel$habitat[i] == "prairies") {DJ[i,16]=1}
     if (champ_sel$habitat[i] == "sentier") {DJ[i,17]=1}
     if (champ_sel$habitat[i] == "urbain") {DJ[i,18]=1}
    }
colnames(DJ) <- c("ferme","serre","blanc","gris","jaune","marron","rouge","abime","non","amande","anis","apre","inodore","foret","pelouse","prairies","sentier","urbain")
rownames(DJ) <- rownames(champignons)

s_Zubin <- matrix(0,nrow=n,ncol=n)
d_prop <- matrix(0,nrow=n,ncol=n)
d_Zubin <- matrix(0,nrow=n,ncol=n)
d_mixte <- matrix(0,nrow=n,ncol=n)
for (i in 1:n)
    {for (j in 1:n)
         {d_prop[i,j]=(abs(DJ[i,3]-DJ[j,3])+abs(DJ[i,4]-DJ[j,4])+abs(DJ[i,5]-DJ[j,5])+abs(DJ[i,6]-DJ[j,6])+abs(DJ[i,10]-DJ[j,10])+abs(DJ[i,11]-DJ[j,11])+abs(DJ[i,12]-DJ[j,12])+abs(DJ[i,13]-DJ[j,13])+abs(DJ[i,14]-DJ[j,14])+abs(DJ[i,15]-DJ[j,15])+abs(DJ[i,16]-DJ[j,16])+abs(DJ[i,17]-DJ[j,17])+abs(DJ[i,18]-DJ[j,18]))/6
          if (i == j) {d_prop[i,j]=0}
          if ((DJ[i,1] == 1 & DJ[j,1] == 1) | (DJ[i,1] == 0 & DJ[j,1] == 0)) {s_Zubin[i,j]=s_Zubin[i,j]+1}
          if ((DJ[i,8] == 1 & DJ[j,8] == 1) | (DJ[i,8] == 0 & DJ[j,8] == 0)) {s_Zubin[i,j]=s_Zubin[i,j]+1}
          s_Zubin[i,j]=s_Zubin[i,j]/2
          d_Zubin[i,j]=1-s_Zubin[i,j]
          if (i == j) {d_Zubin[i,j]=0}
          d_mixte[i,j]=(3*d_prop[i,j]+2*d_Zubin[i,j])/5
          if (i == j) {d_mixte[i,j]=0}
         }
    }
rownames(d_mixte) <- rownames(champignons)
colnames(d_mixte) <- rownames(champignons)

Application de l’analyse des correspondances multiples

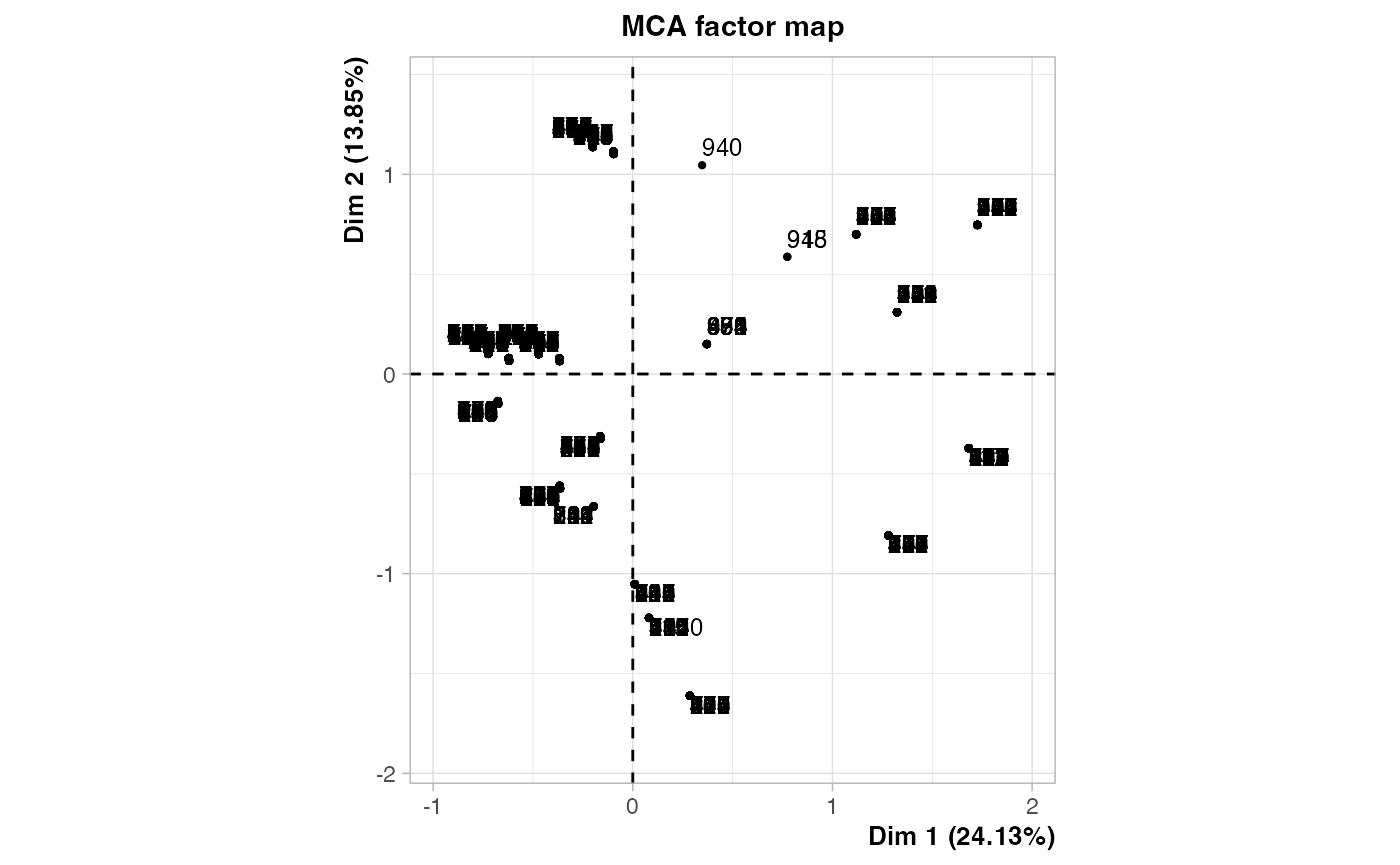
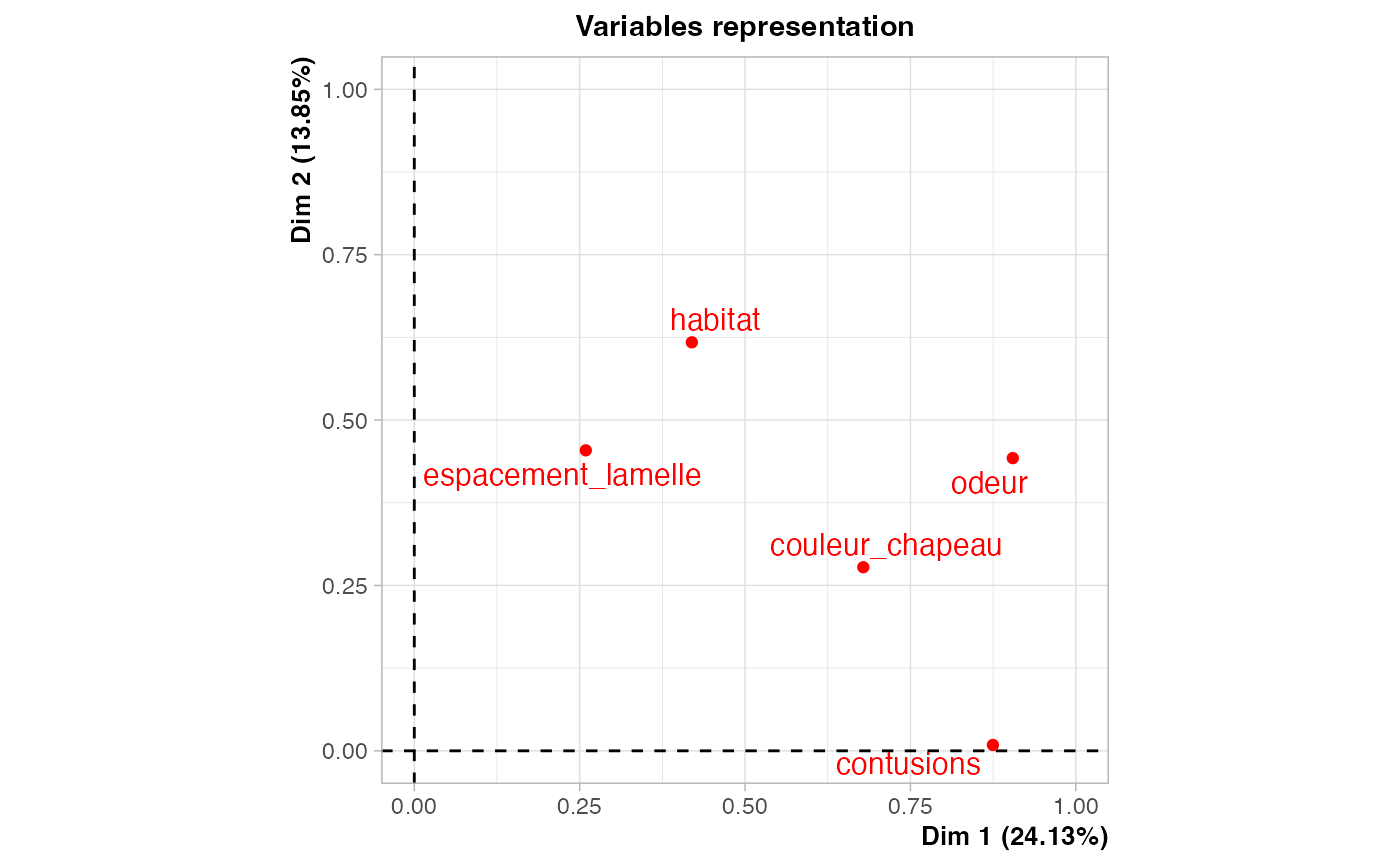
res.ACM <- FactoMineR::MCA(champ_sel)
#> Warning: ggrepel: 1 unlabeled data points (too many overlaps). Consider
#> increasing max.overlaps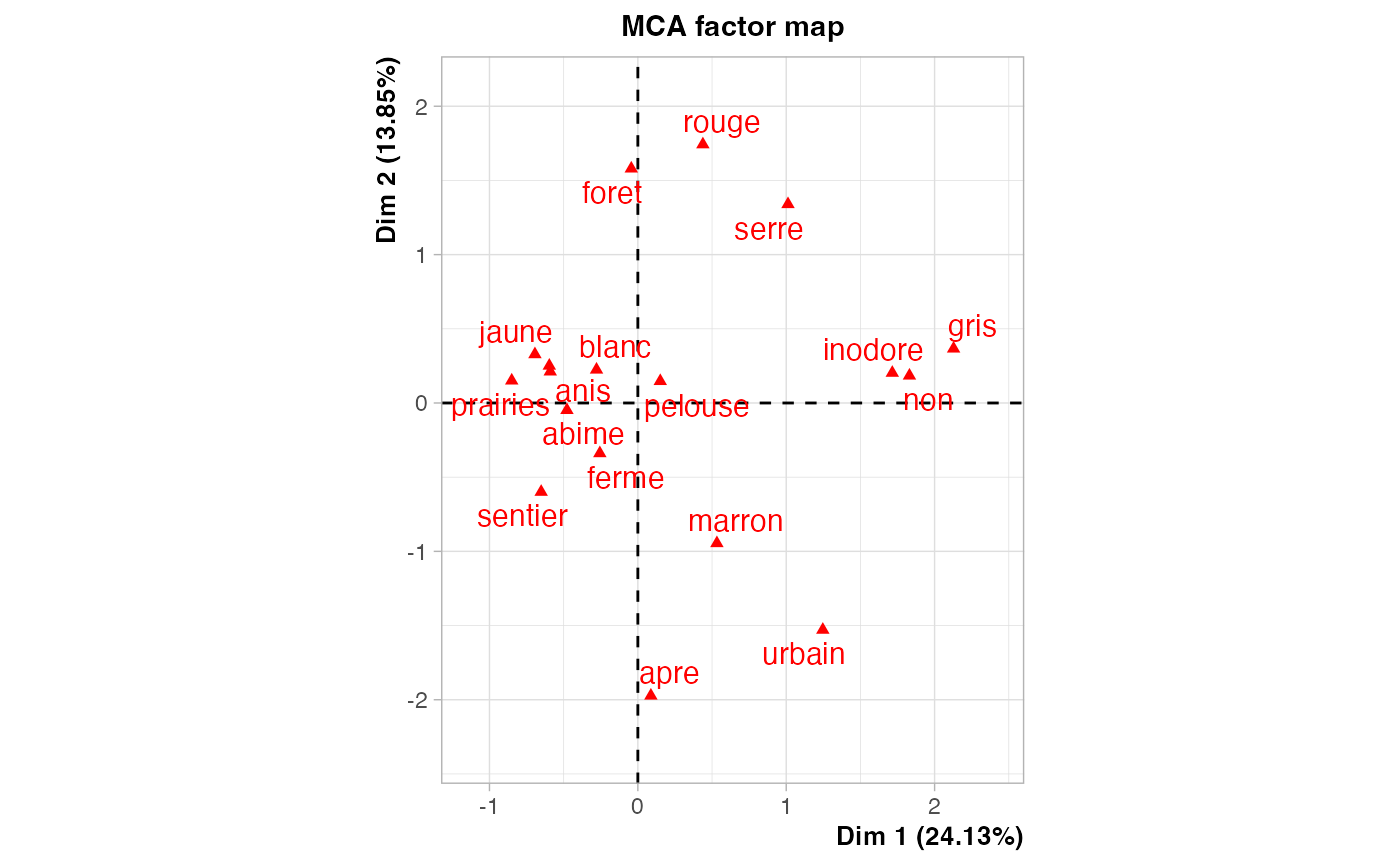

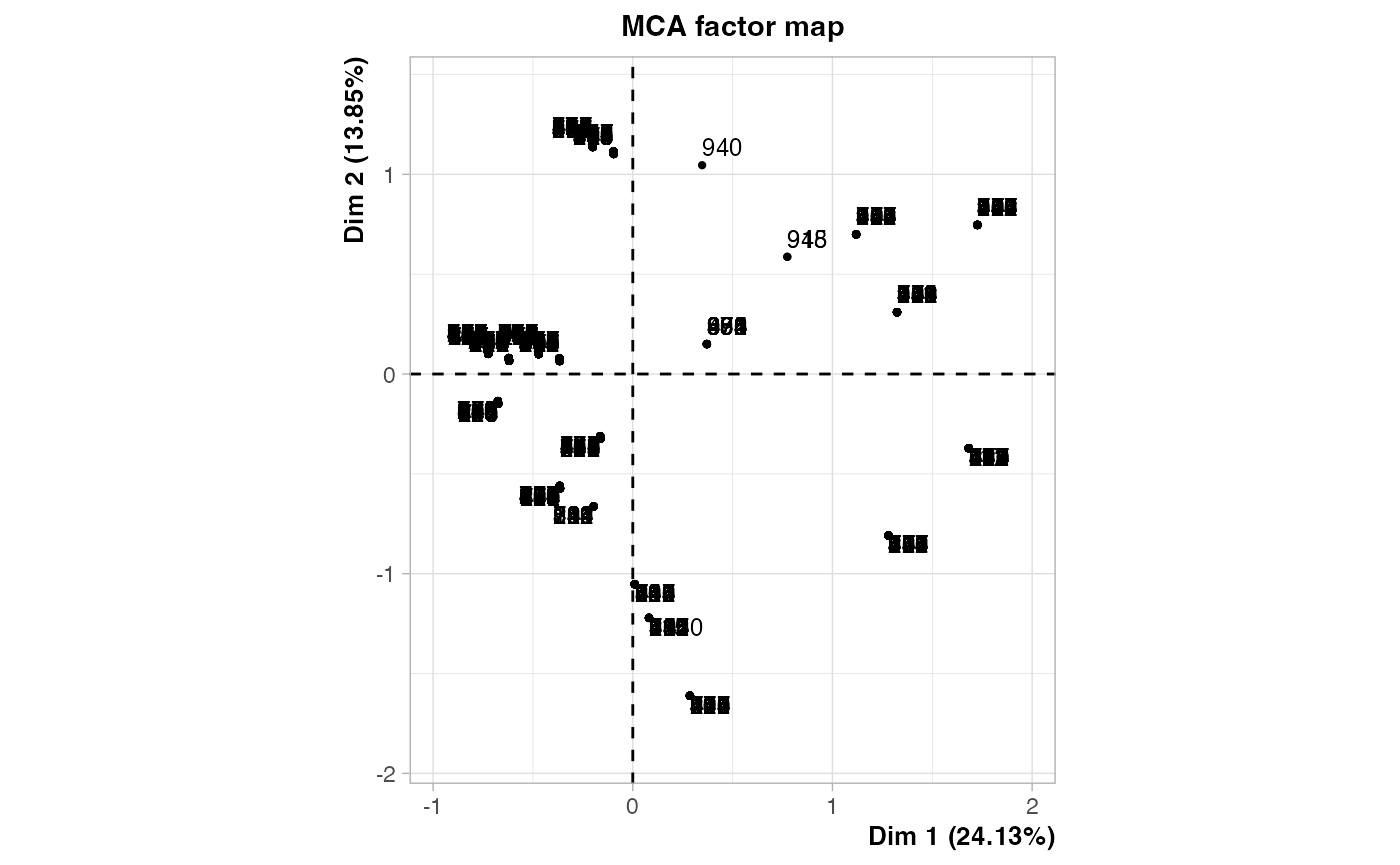
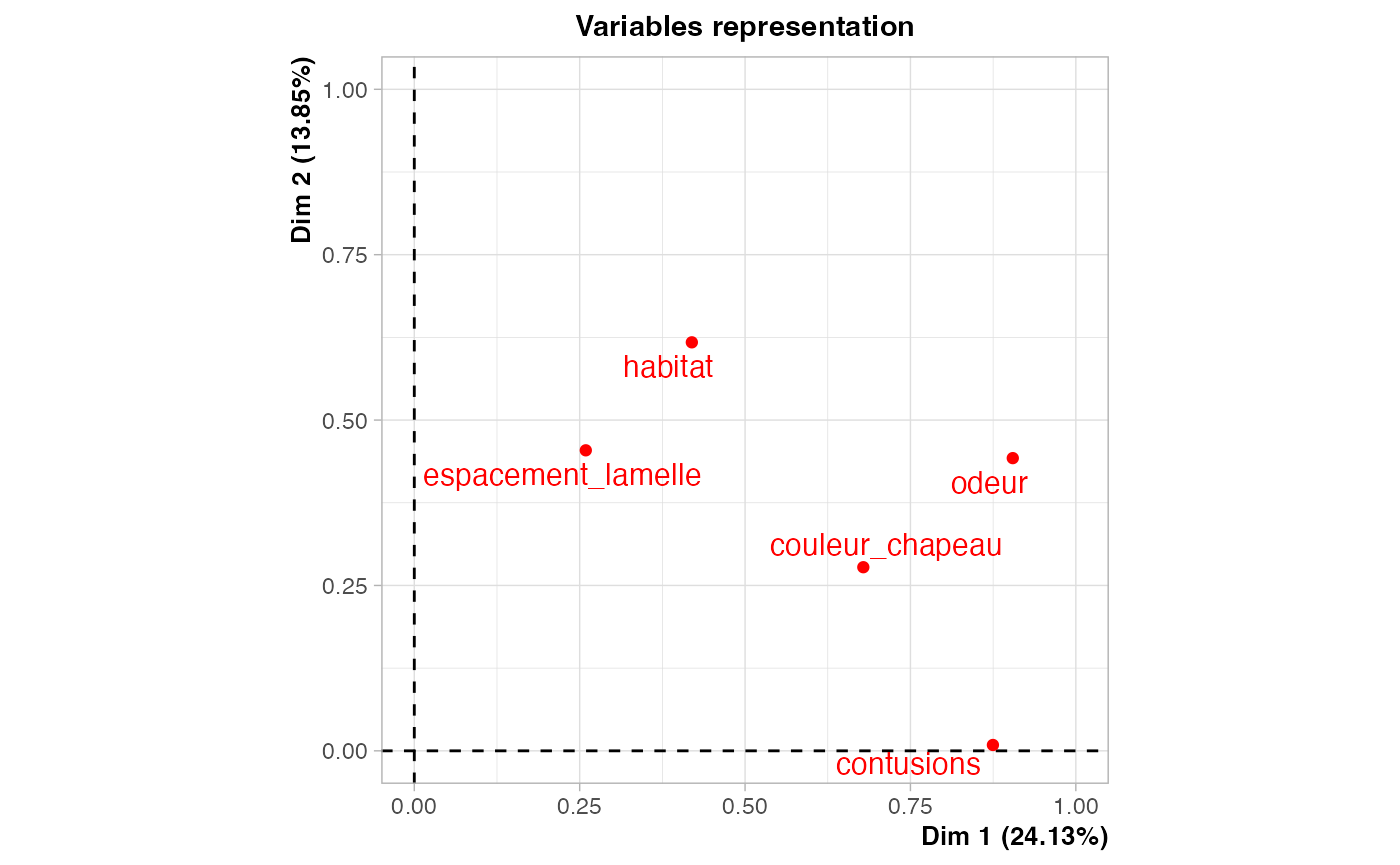
Nombre de composantes principales résumant au moins 80 % de l’inertie

eig.val <- res.ACM$eig

Calcul des distances euclidiennes sur les sept premières composantes principales

res.ACM <- FactoMineR::MCA(champ_sel,ncp=7)
#> Warning: ggrepel: 1 unlabeled data points (too many overlaps). Consider
#> increasing max.overlaps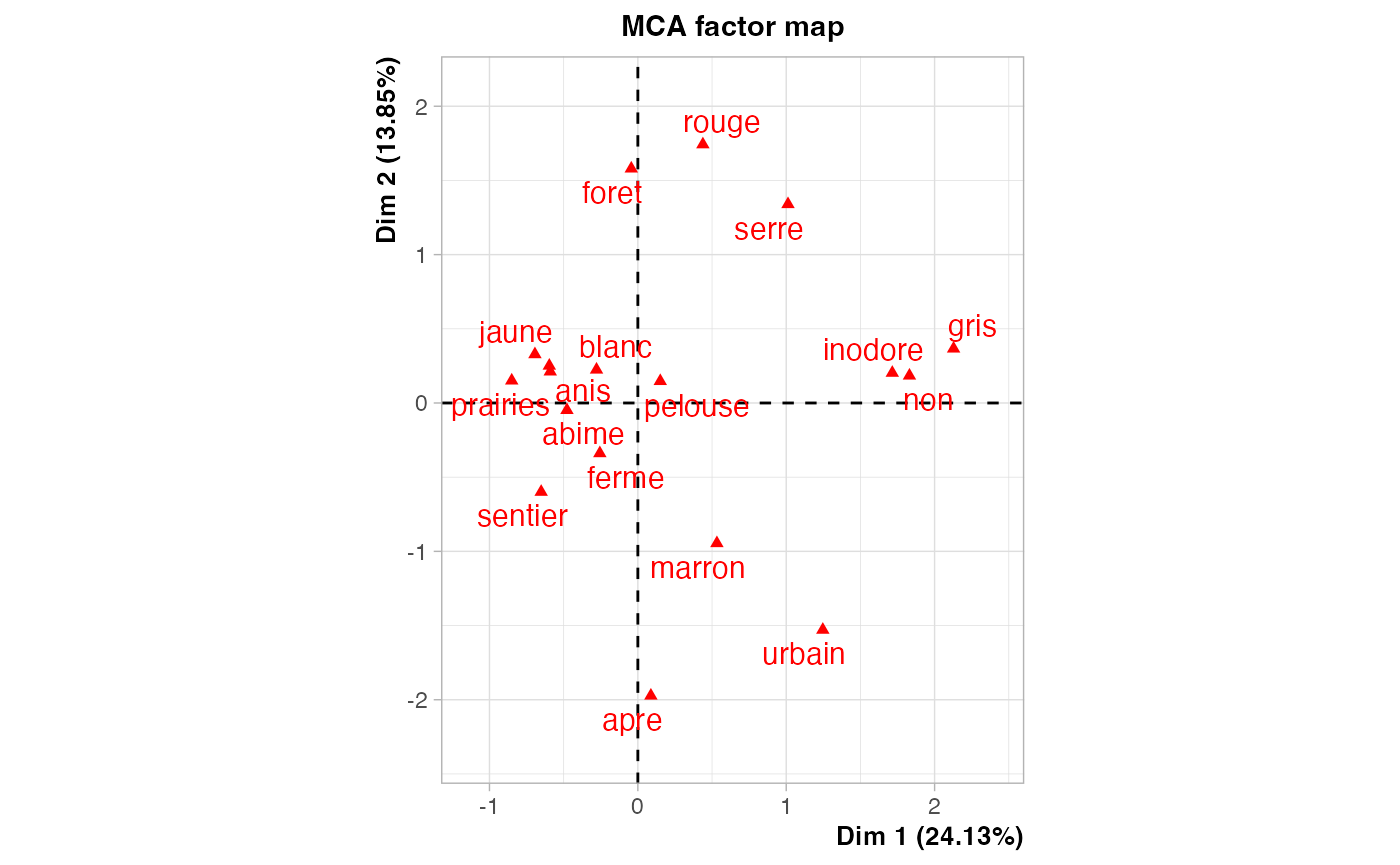

champ_MCA <- res.ACM$ind$coord
d.champ_ACM <- dist(champ_MCA)

Exercice 7.3 : Application de la classification hiérarchique ascendante de Ward sur les données de pollution de l’air au Etats-Unis

Description des données

Échantillon de 50 villes (individus) tirées aléatoirement sur la pollution de l’air aux Etats-Unis en 1960

CITY : Nom de la ville
TMR : taux de mortalité exprimé en 1/10000
GE65 : pourcentage (multiplié par 10) de la population des 65 ans et plus
LPOP : logarithme (en base 10 et multiplié par 10) de la population
NONPOOR : pourcentage de ménages avec un revenu au dessus du seuil de pauvreté
PERWH : pourcentage de population blanche
PMEAN : moyenne arithmétique des relevés réalisés deux fois par semaine de particules suspendues dans l’air (micro-g/m3 multiplié par 10)
PMIN : plus petite valeur des relevés réalisés deux fois par semaine de particules suspendues dans l’air (micro-g/m3 multiplié par 10)
LPMAX : logarithme de la plus grande valeur des relevés réalisés deux fois par semaine de particules suspendues dans l’air (micro-g/m3 multiplié par 10)
SMEAN : moyenne arithmétique des relevés réalisés deux fois par semaine de sulfate (micro-g/m3 multiplié par 10)
SMIN : plus petite valeur des relevés réalisés deux fois par semaine de sulfate (micro-g/m3 multiplié par 10)
SMAX : plus grande valeur des relevés réalisés deux fois par semaine de sulfate (micro-g/m3 multiplié par 10)
LPM2 : logarithme de la densité de la population par mile carré (multiplié par 0,1)

Lecture des données

data(air_pollution)

Elimine les variables PM2 et PMAX qui sont transformées en logarithme dans les variables l_pm2 et l_pmax

air_pollution <- air_pollution[,-(8:9)]

Centrer-réduire les variables sauf TMR et élimination de CITY qui n’est pas numérique

air_pollution_std <- scale(air_pollution[,-(1:2)])
air_pollution_std <- data.frame(air_pollution_std)

Application du critère de Ward sur la matrice des distances euclidiennes à partir des données standadisées

d.air_pol <- dist(air_pollution_std)
cah.ward <- hclust(d.air_pol,method="ward.D2")
cah.ward$height <- cah.ward$height^2/2
plot(cah.ward)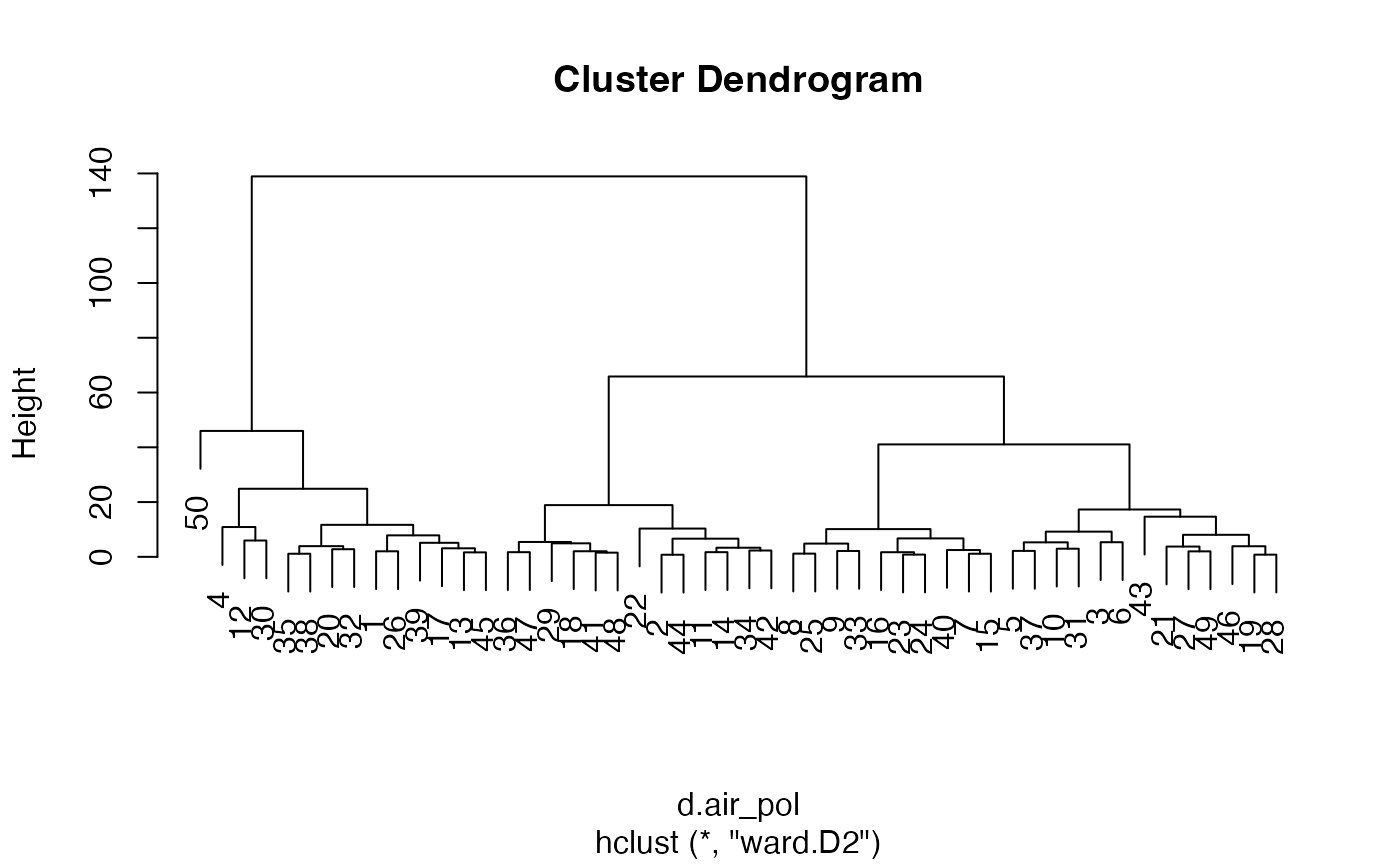

Dendrogramme avec matérialisation des groupes

plot(cah.ward)
rect.hclust(cah.ward,k=5)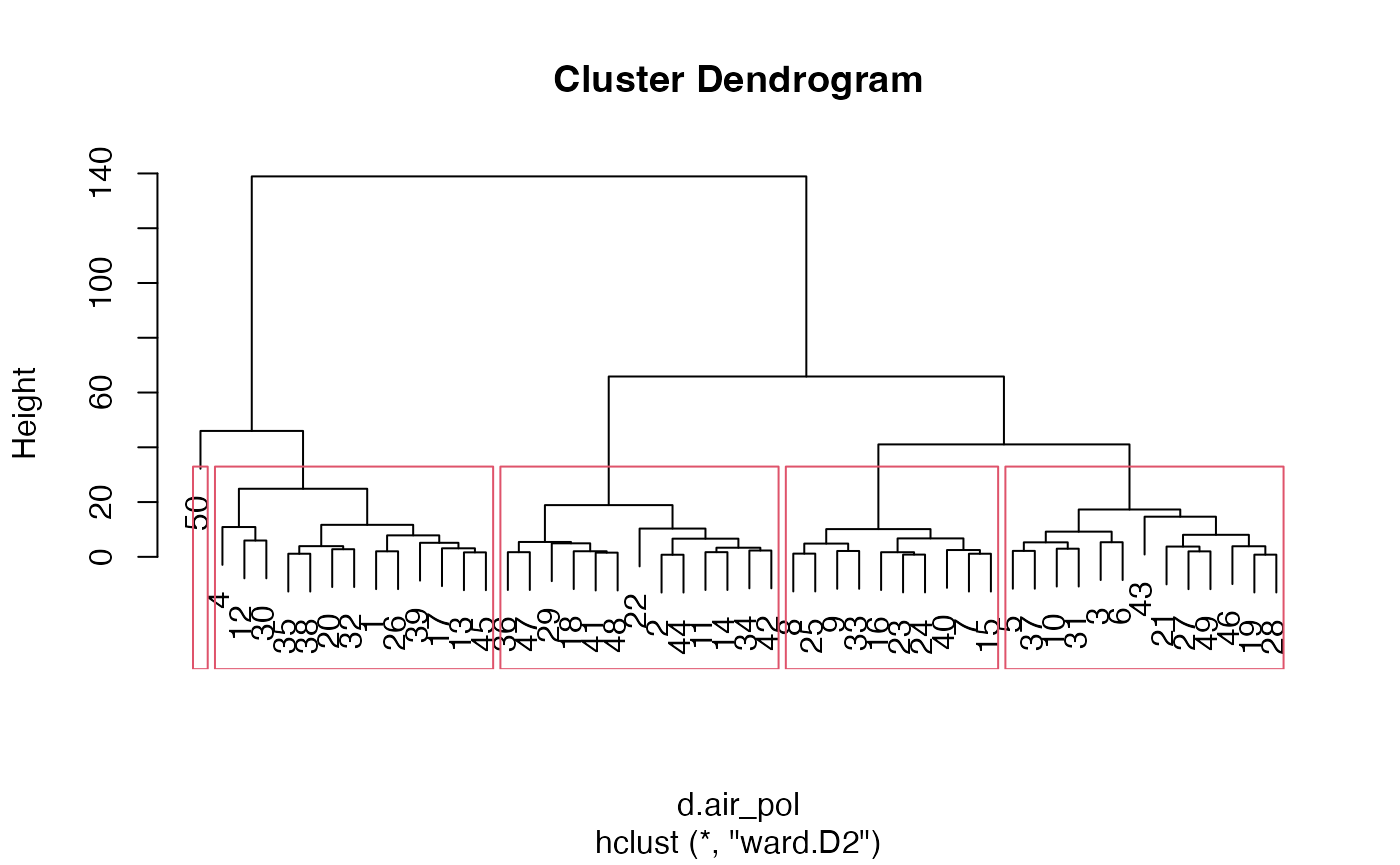

Découpage en 5 groupes

groupes.cah_ward_DS <- cutree(cah.ward,k=5)

Application du critère de Ward sur la matrice des distances euclidiennes à partir des composantes principales retenues

res.PCA <- FactoMineR::PCA(air_pollution[,-(1:2)],ncp=4)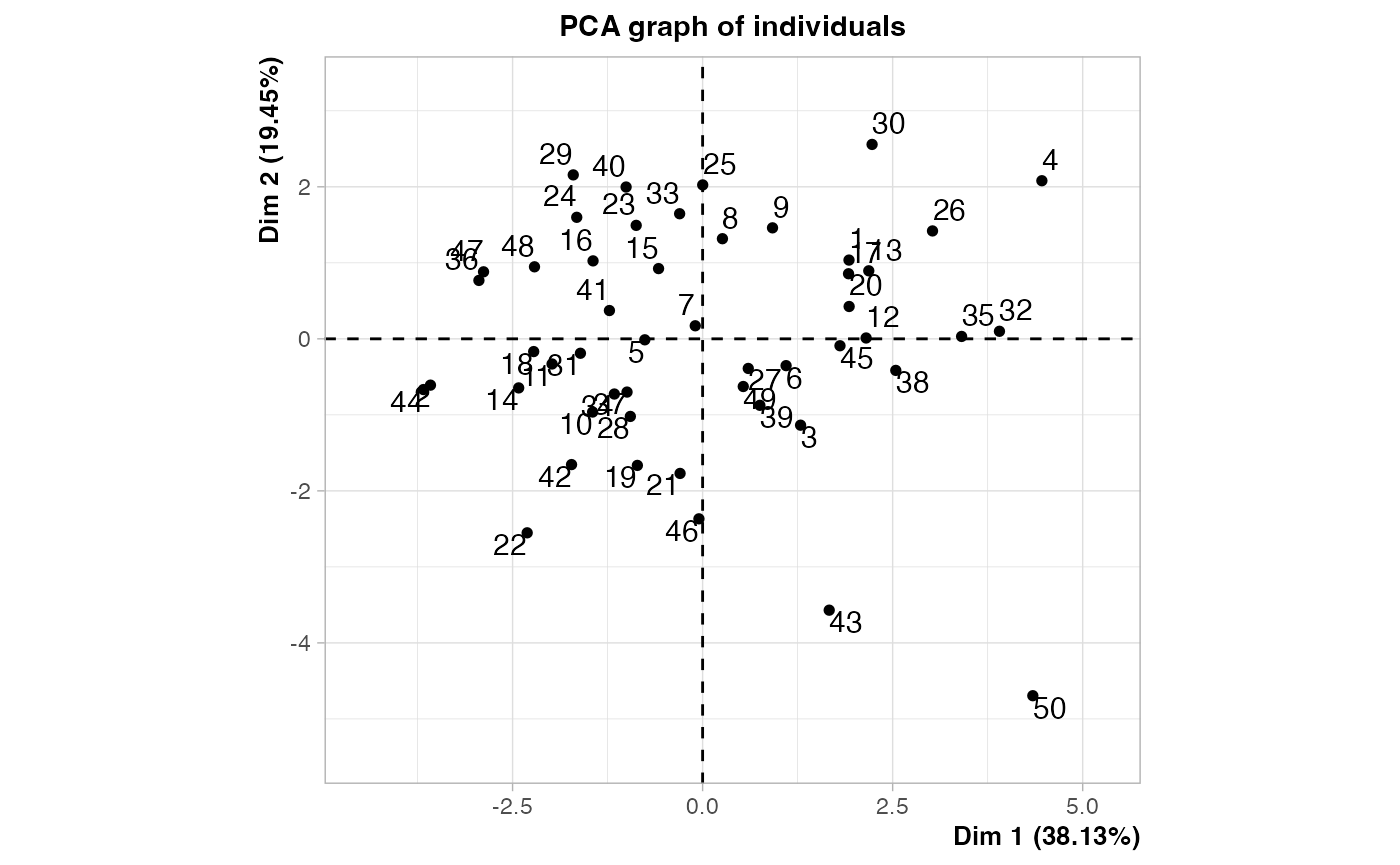

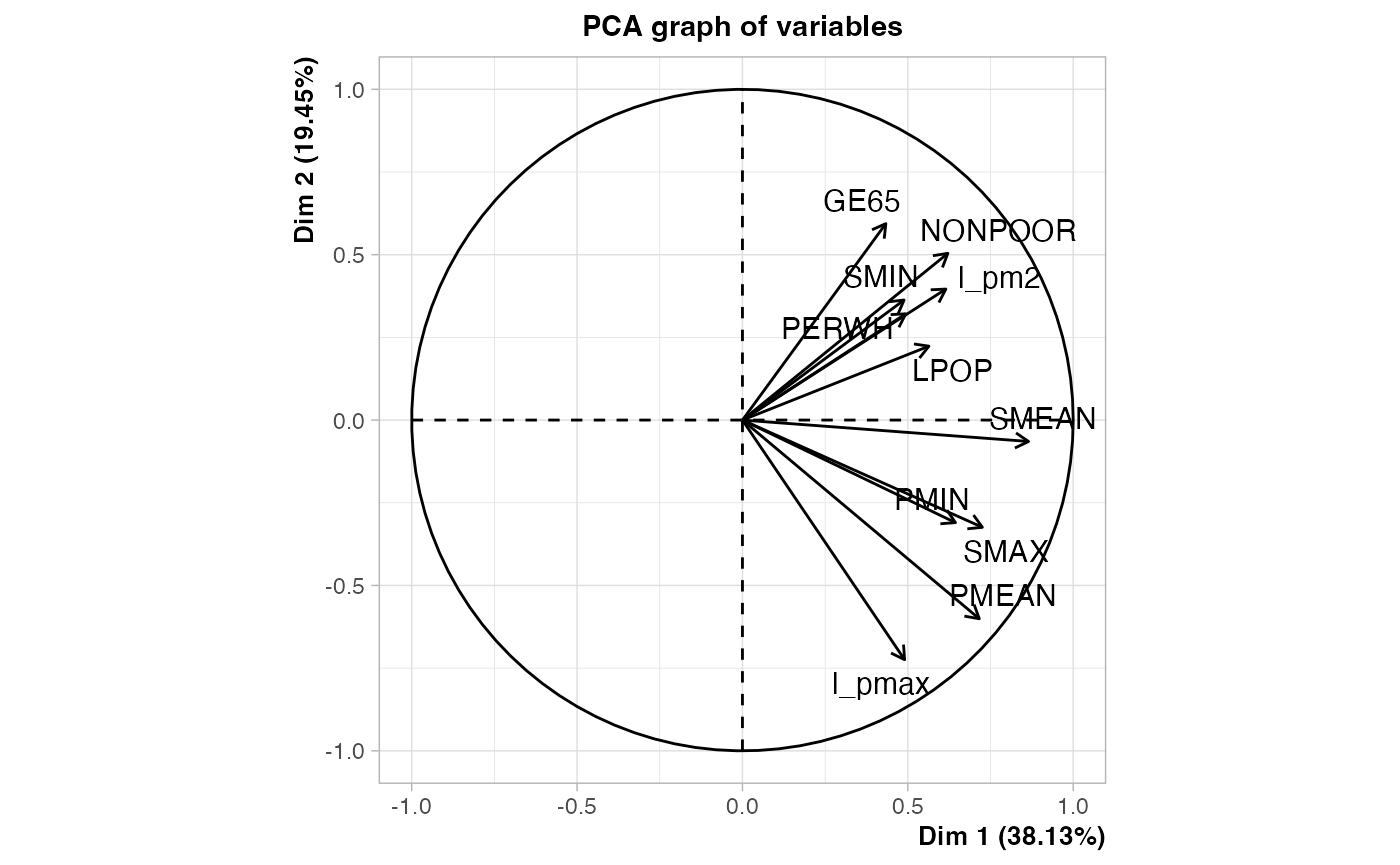
air_pol_PCA <- res.PCA$ind$coord
d.air_pol <- dist(air_pol_PCA)
cah.ward <- hclust(d.air_pol,method="ward.D2")
cah.ward$height <- cah.ward$height^2/2

plot(cah.ward)

Dendrogramme avec matérialisation des groupes

plot(cah.ward)
rect.hclust(cah.ward,k=5)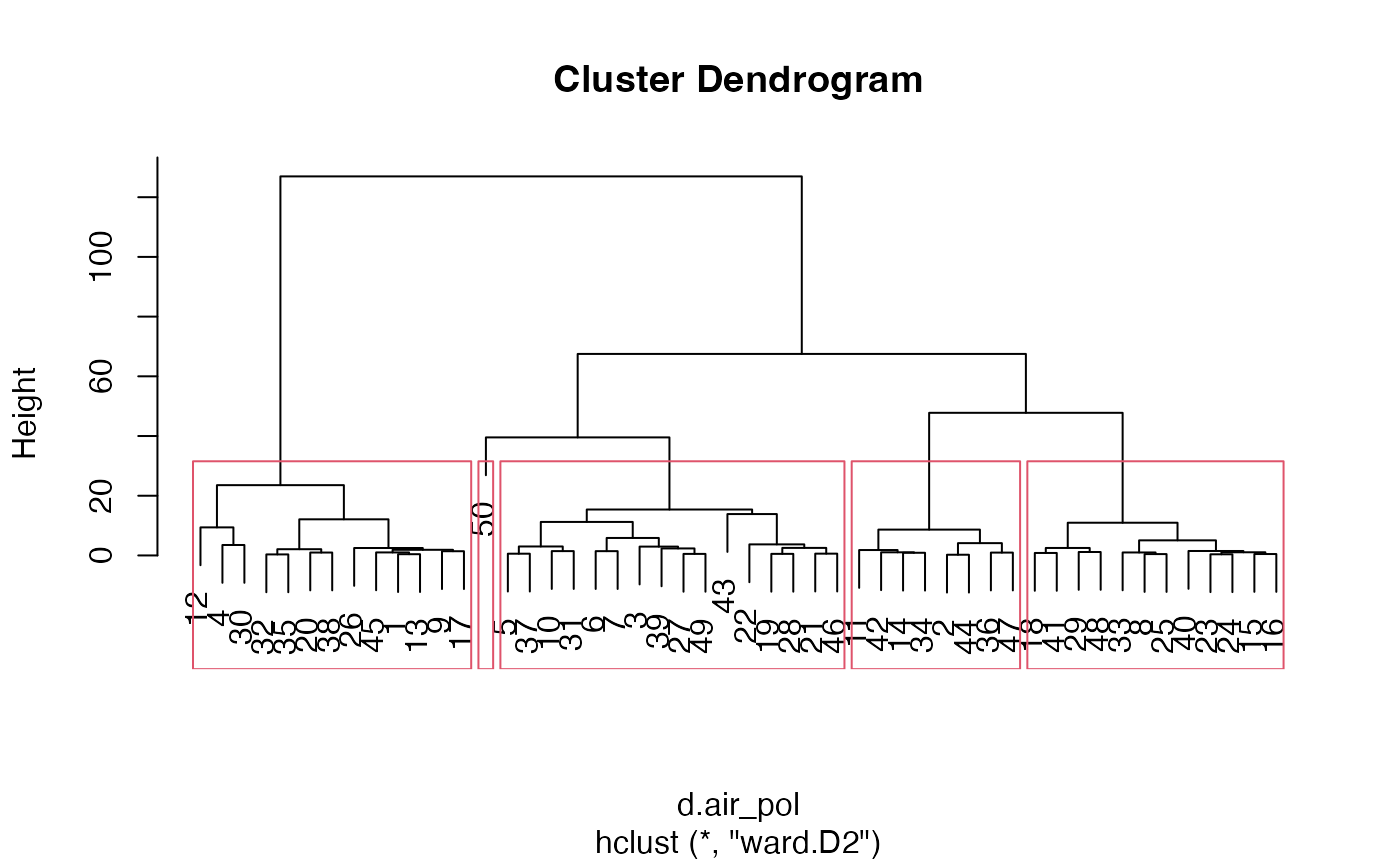

Découpage en 5 groupes

groupes.cah_ward_PCA <- cutree(cah.ward,k=5)

Exercice 7.4 : Application de la classification hiérarchique ascendante de Ward sur les données de caractéristiques des champignons

Application du critère de Ward sur la matrice de dissimilarités mixtes et choix du nombre de classes adéquat

arbre2 <- cluster::agnes(d_mixte, method = "ward")
cah.ward <- as.hclust(arbre2)
cah.ward$height <- cah.ward$height^2/2
plot(cah.ward,labels=FALSE)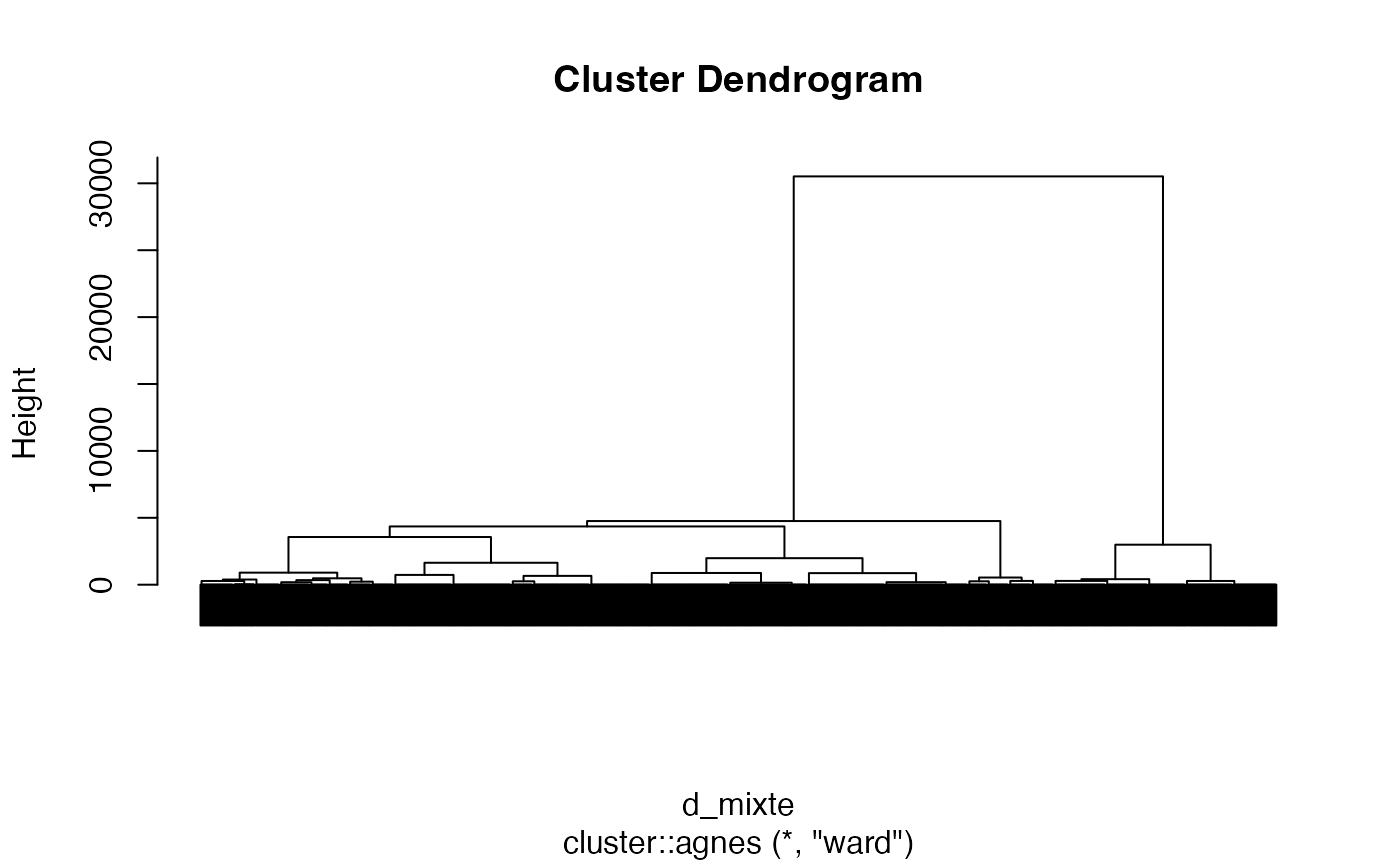

Affiche la décroissance de l’inertie expliquée

inertie <- sort(cah.ward$height, decreasing = TRUE)
plot(inertie[1:30], type = "s", xlab = "Nombre de classes", ylab = "Inertie")
points(c(2, 6, 8), inertie[c(2, 6, 8)], col = c("green3", "red3", "blue3"), cex = 2, lwd = 3)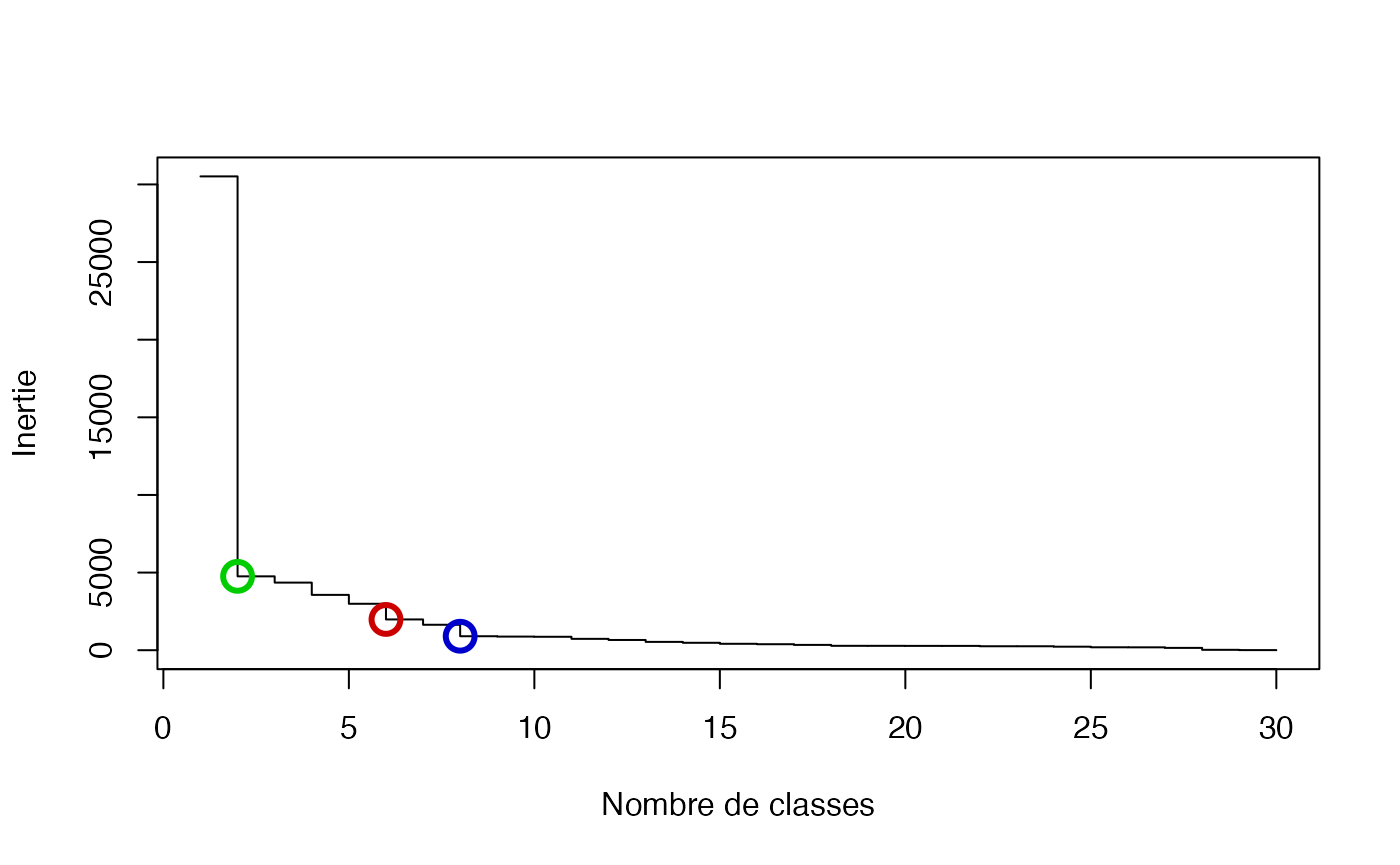

Dendrogramme avec matérialisation des groupes

plot(cah.ward,labels=FALSE)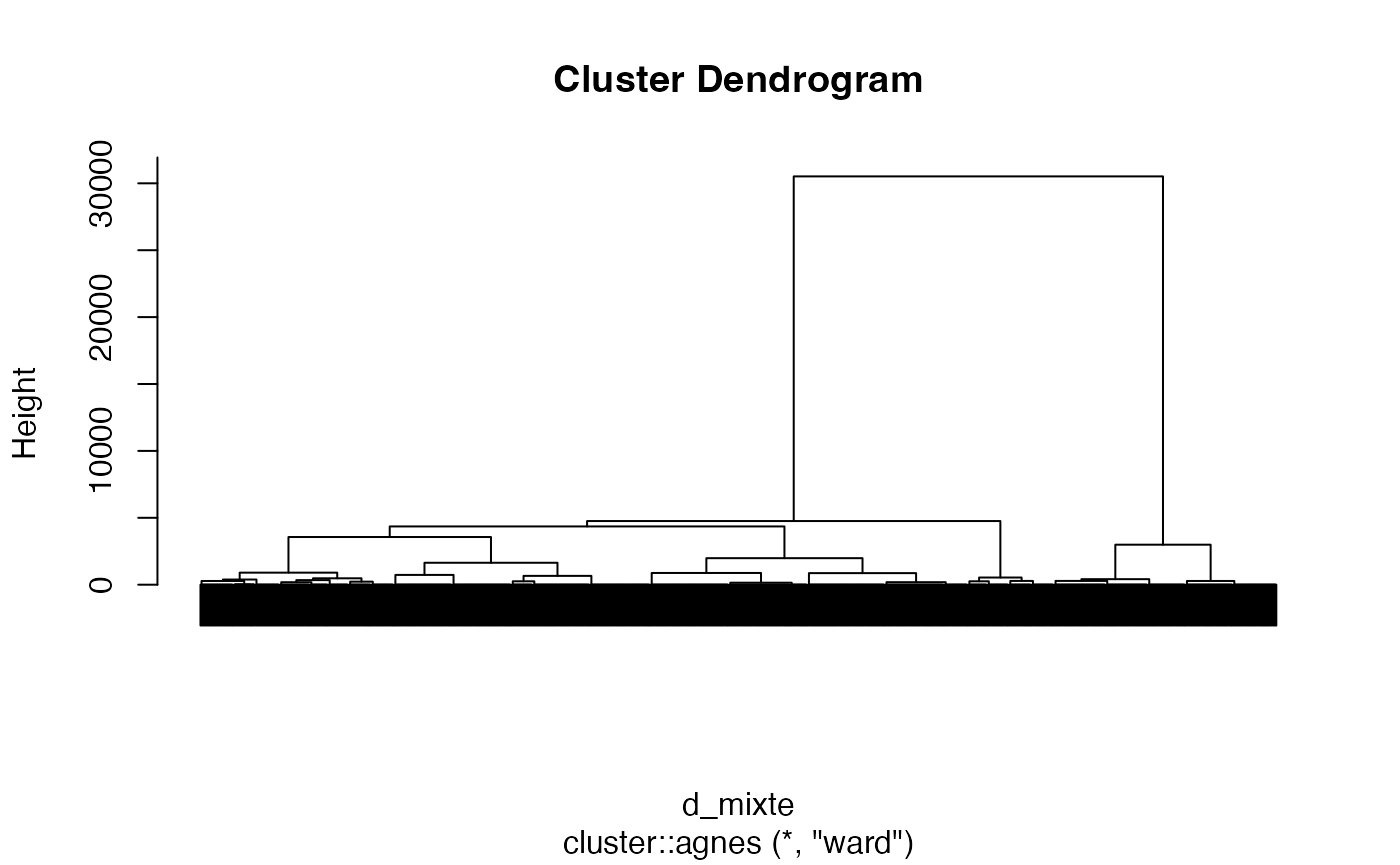

Découpage en 6 groupes

plot(cah.ward,labels=FALSE)
rect.hclust(cah.ward,k=6)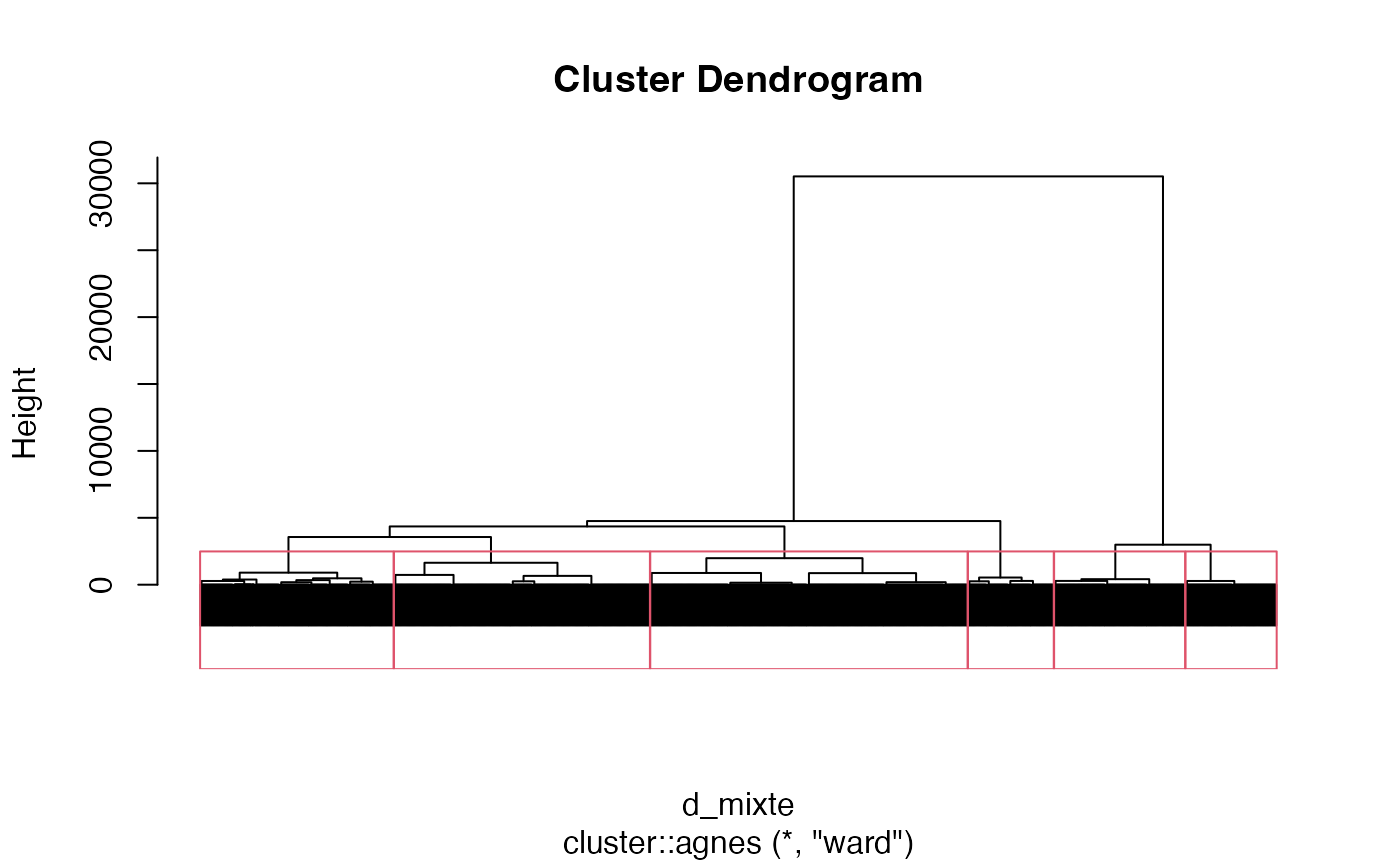

plot(cah.ward,labels=FALSE)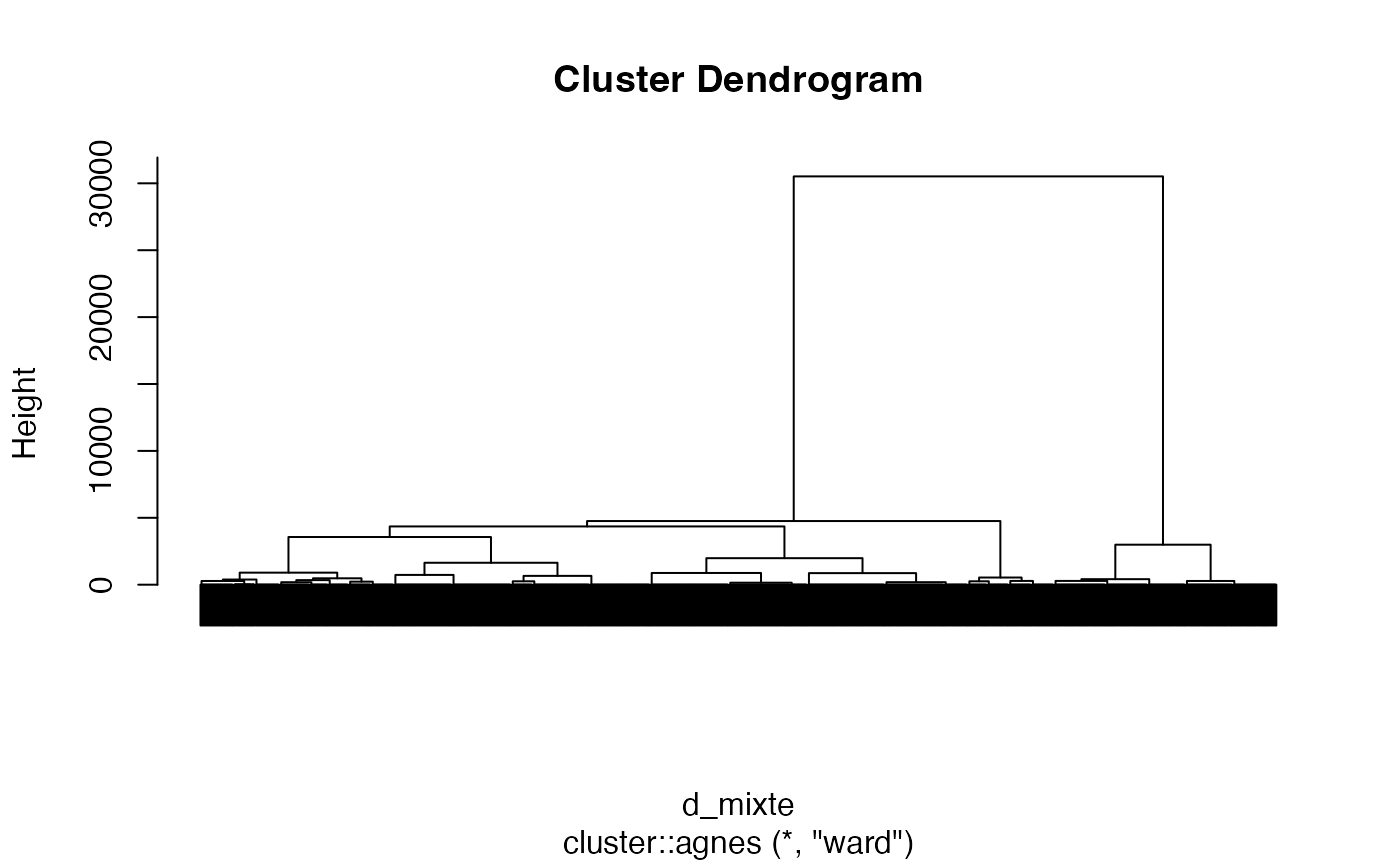

groupes.cah_ward_d_mixte_6 <- cutree(cah.ward,k=6)

Découpage en 8 groupes

plot(cah.ward,labels=FALSE)
rect.hclust(cah.ward,k=8)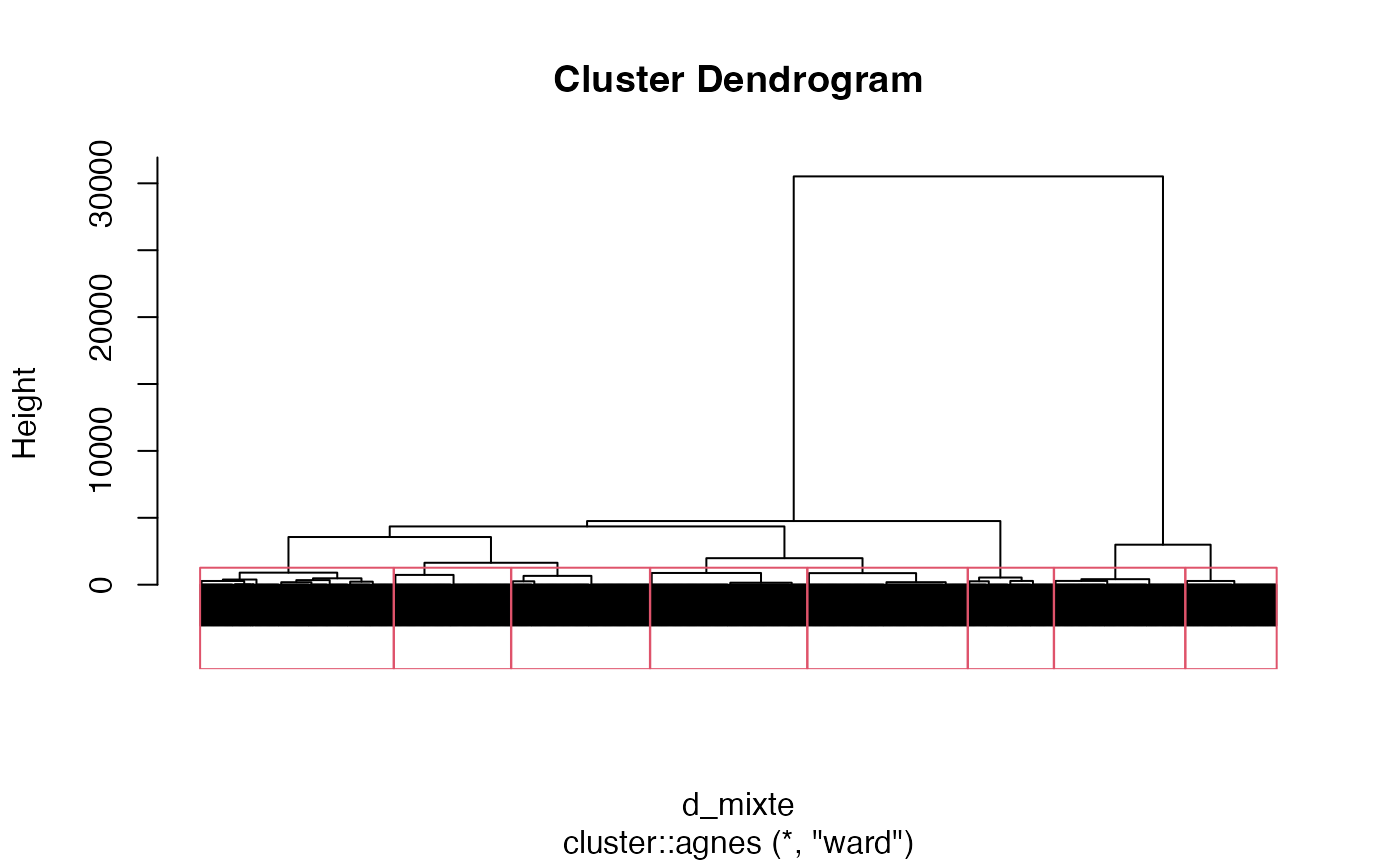

groupes.cah_ward_d_mixte_8 <- cutree(cah.ward,k=8)

Application du critère de Ward sur la matrice des distances euclidiennes à partir des composantes principales retenues

arbre2 <- cluster::agnes(d.champ_ACM, method = "ward")
cah.ward_ACM <- as.hclust(arbre2)
cah.ward_ACM$height <- cah.ward_ACM$height^2/2
plot(cah.ward_ACM,labels=FALSE)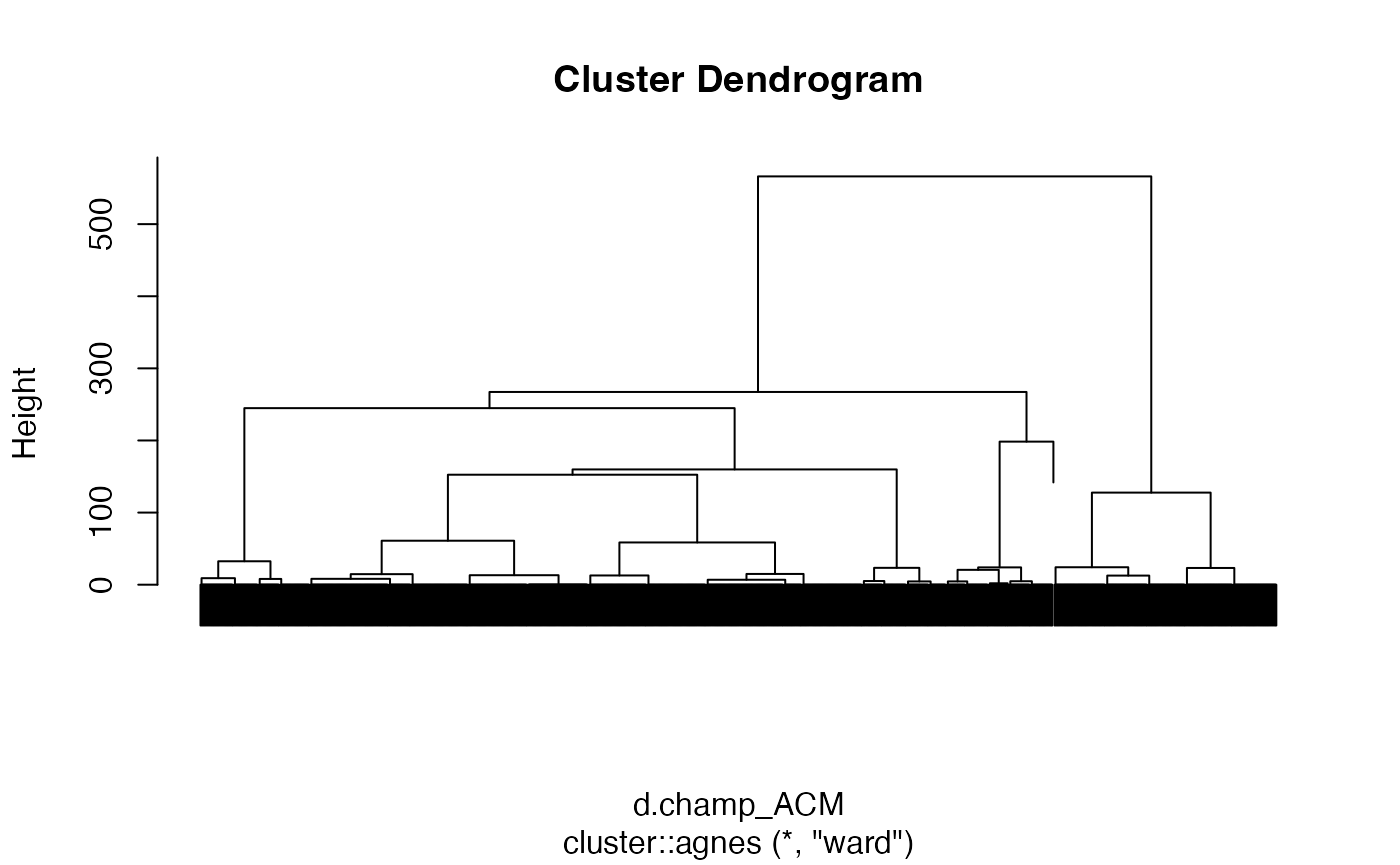

Affiche la décroissance de l’inertie expliquée

inertie <- sort(cah.ward_ACM$height, decreasing = TRUE)
plot(inertie[1:30], type = "s", xlab = "Nombre de classes", ylab = "Inertie")
points(c(2, 4, 5, 8), inertie[c(2, 4, 5, 8)], col = c("green3", "red3", "blue3", "orange"), cex = 2, lwd = 3)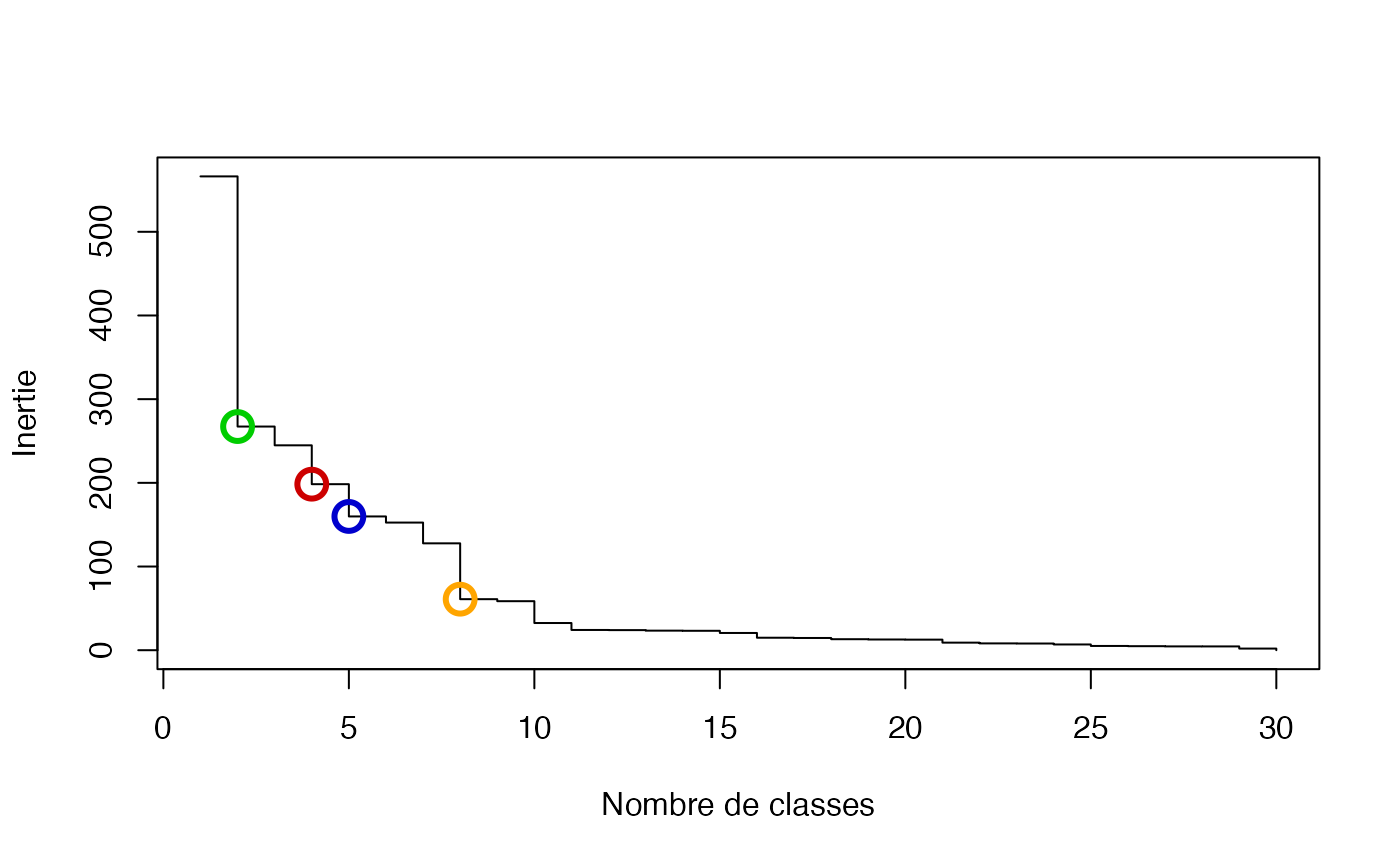

Dendrogramme avec matérialisation des groupes

Découpage en 8 groupes

plot(cah.ward_ACM,labels=FALSE)
rect.hclust(cah.ward_ACM,k=8)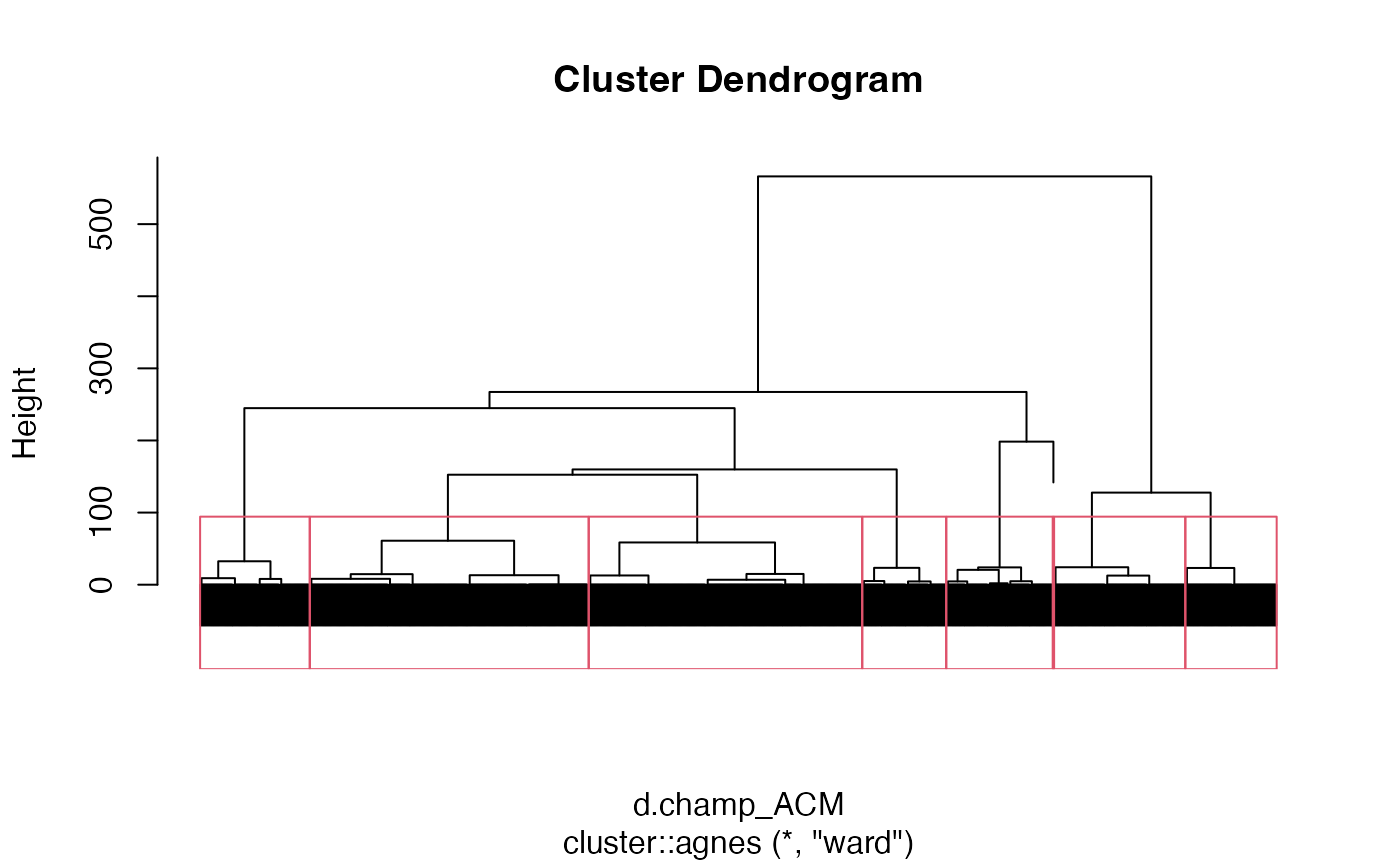

groupes.cah_ward_d_ACM <- cutree(cah.ward_ACM,k=8)

Compararaison de partitions (dissim mixte à 6 classes vs distance euclidienne à 8 classes)

Ward ACM vs Ward d_mixte

T_C <- table(groupes.cah_ward_d_ACM,groupes.cah_ward_d_mixte_6)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2 # apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2 # apply(T_C,2,sum,na.rm=TRUE)^2
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Compararaison de partitions (dissim mixte à 8 classes vs distance euclidienne à 8 classes)

Ward ACM vs Ward d_mixte

T_C <- table(groupes.cah_ward_d_mixte_8,groupes.cah_ward_d_ACM)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2 # apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2 # apply(T_C,2,sum,na.rm=TRUE)^2
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Exercice 7.5 : Application de la classification hiérarchique à d’autres critères sur les données champignons

Critère Complete

arbre2 <- cluster::agnes(d_mixte, method = "complete")
cah.complete <- as.hclust(arbre2)
plot(cah.complete,labels=FALSE)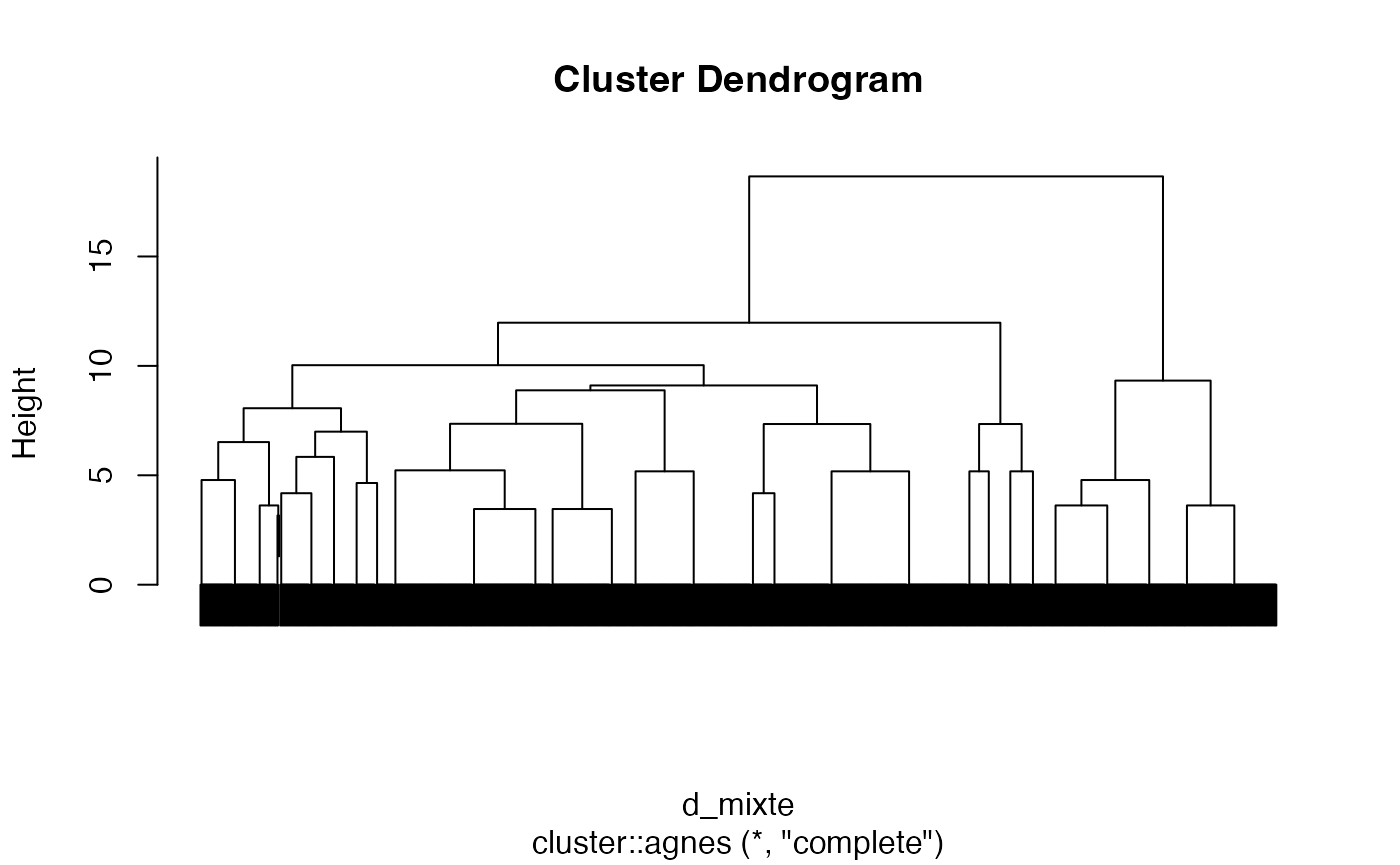

Affiche la décroissance de l’inertie expliquée

inertie <- sort(cah.complete$height, decreasing = TRUE)
plot(inertie[1:30], type = "s", xlab = "Nombre de classes", ylab = "Inertie")
points(c(2, 3, 7, 8), inertie[c(2, 3, 7, 8)], col = c("green3", "red3", "blue3", "orange3"), cex = 2, lwd = 3)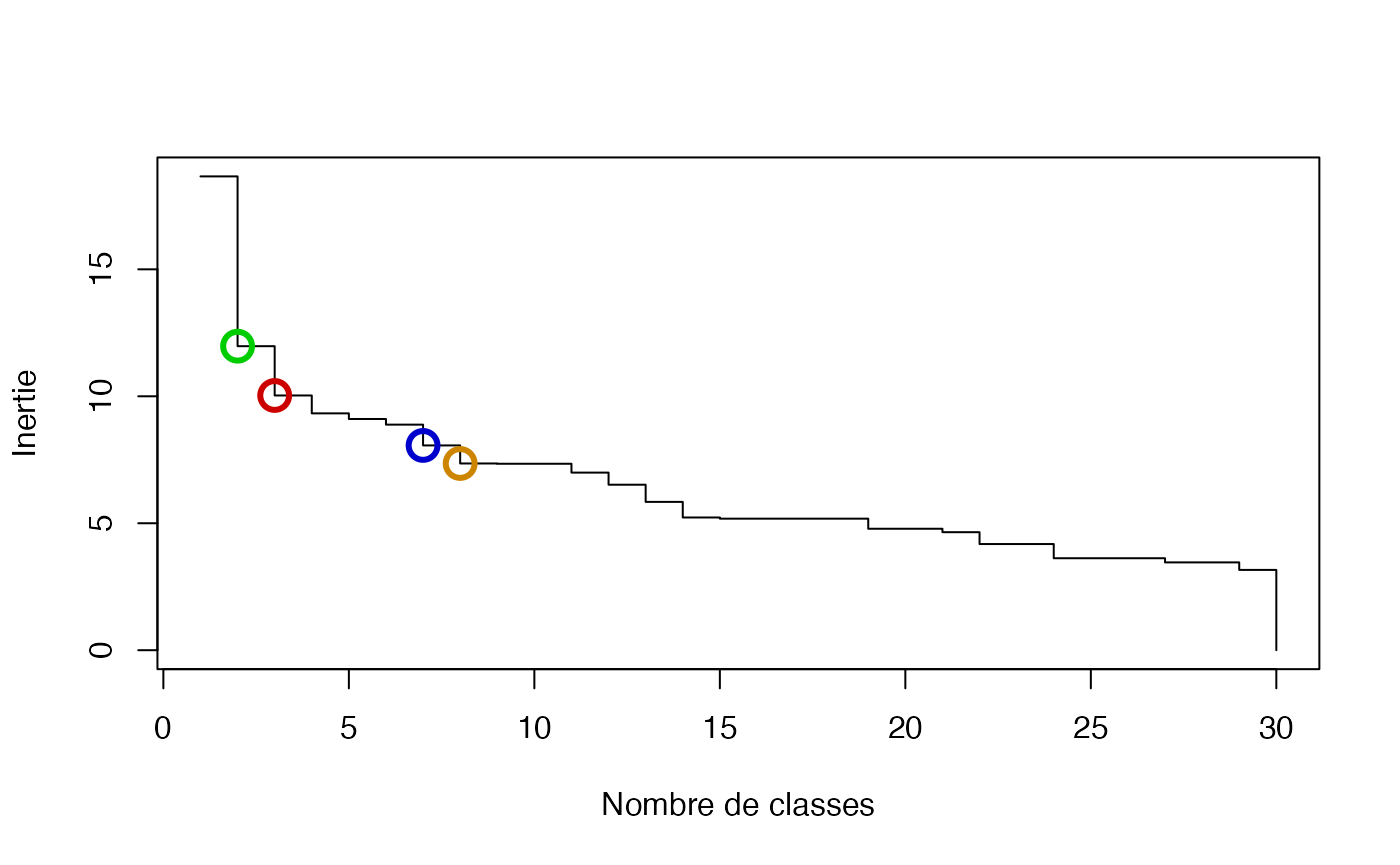

Dendrogramme avec matérialisation des groupes

plot(cah.complete,labels=FALSE)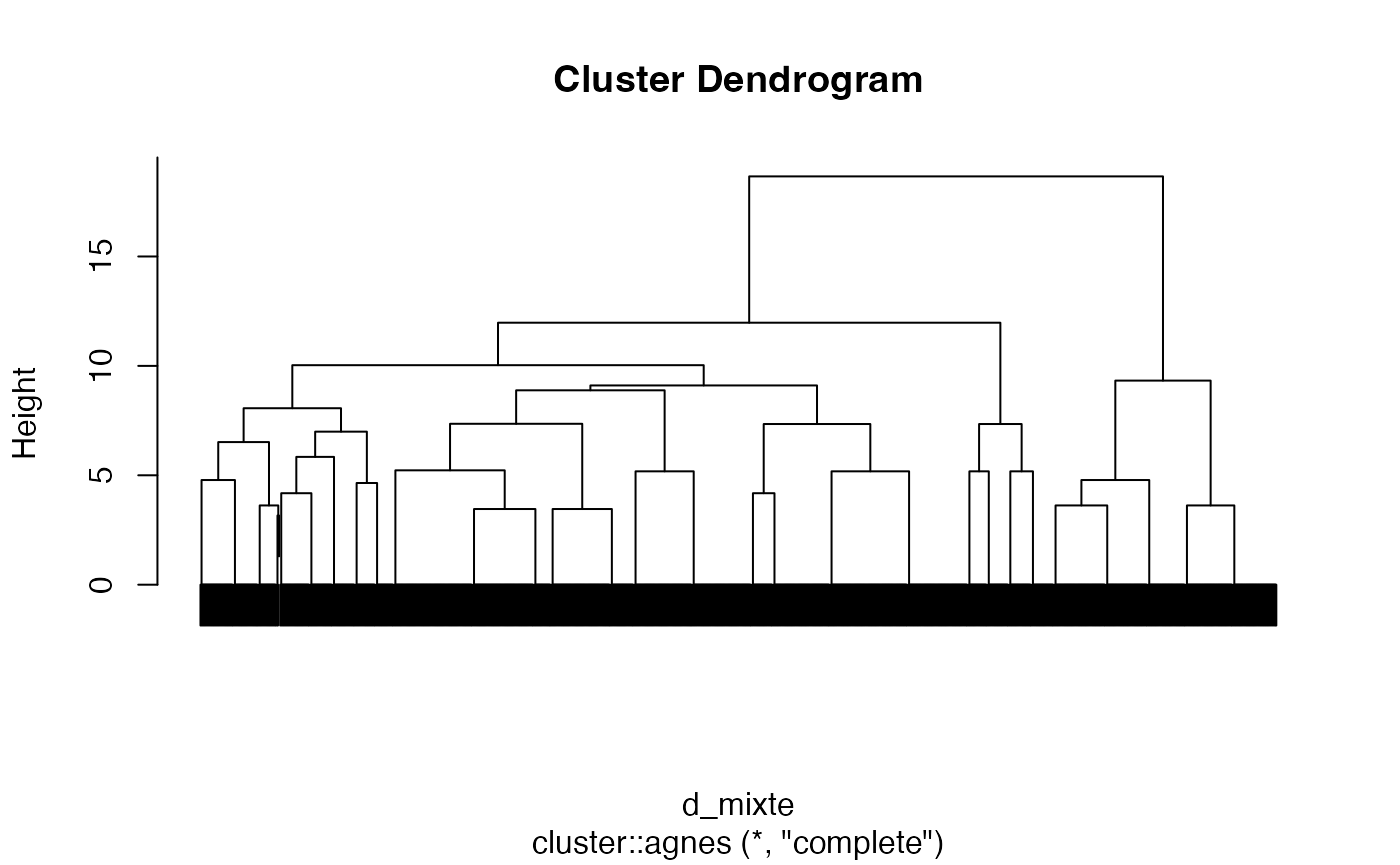

Découpage en 7 groupes

plot(cah.complete,labels=FALSE)
rect.hclust(cah.complete,k=7)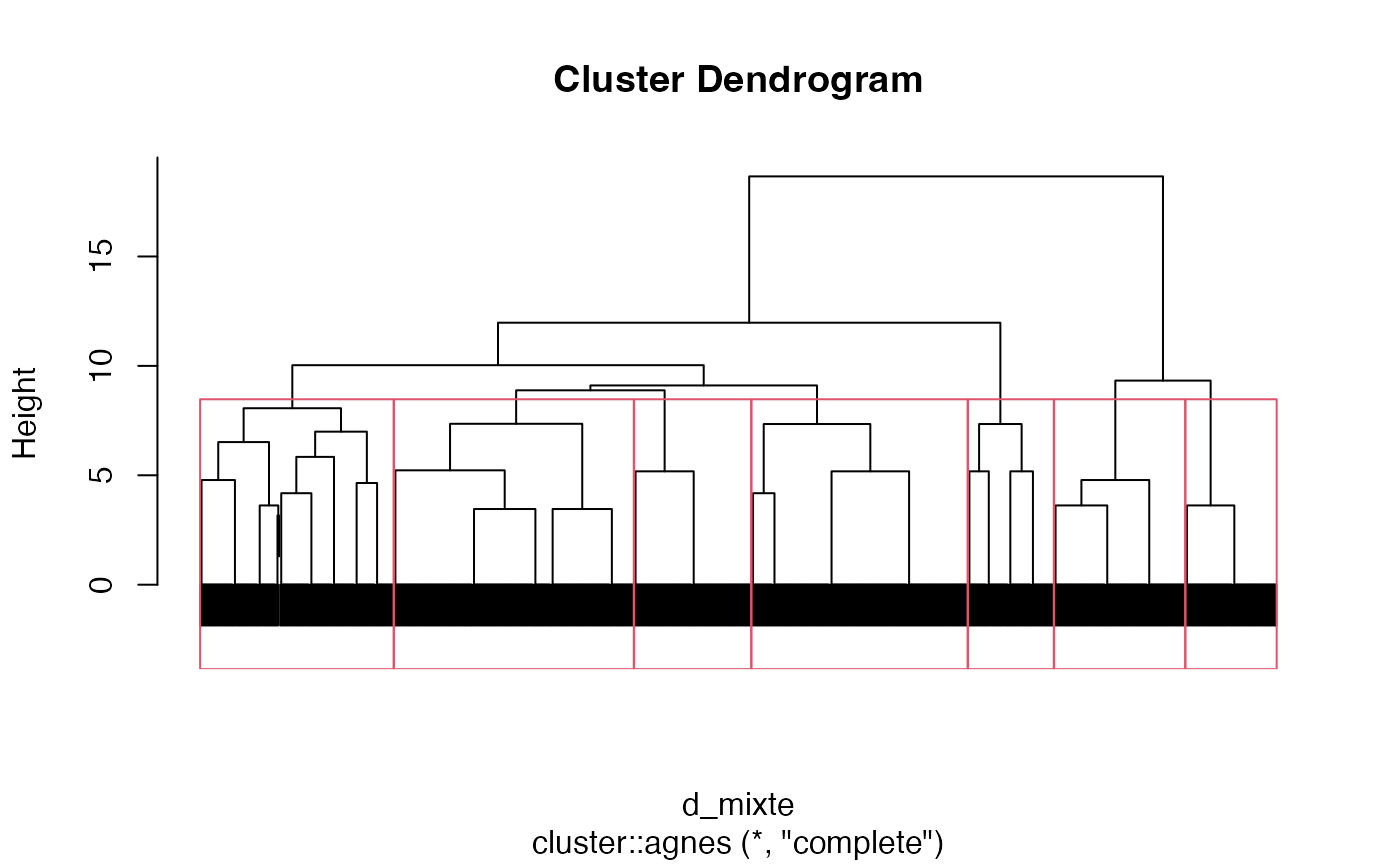

groupes.cah_complete_d_mixte_7 <- cutree(cah.complete,k=7)

Découpage en 8 groupes

plot(cah.complete,labels=FALSE)
rect.hclust(cah.complete,k=8)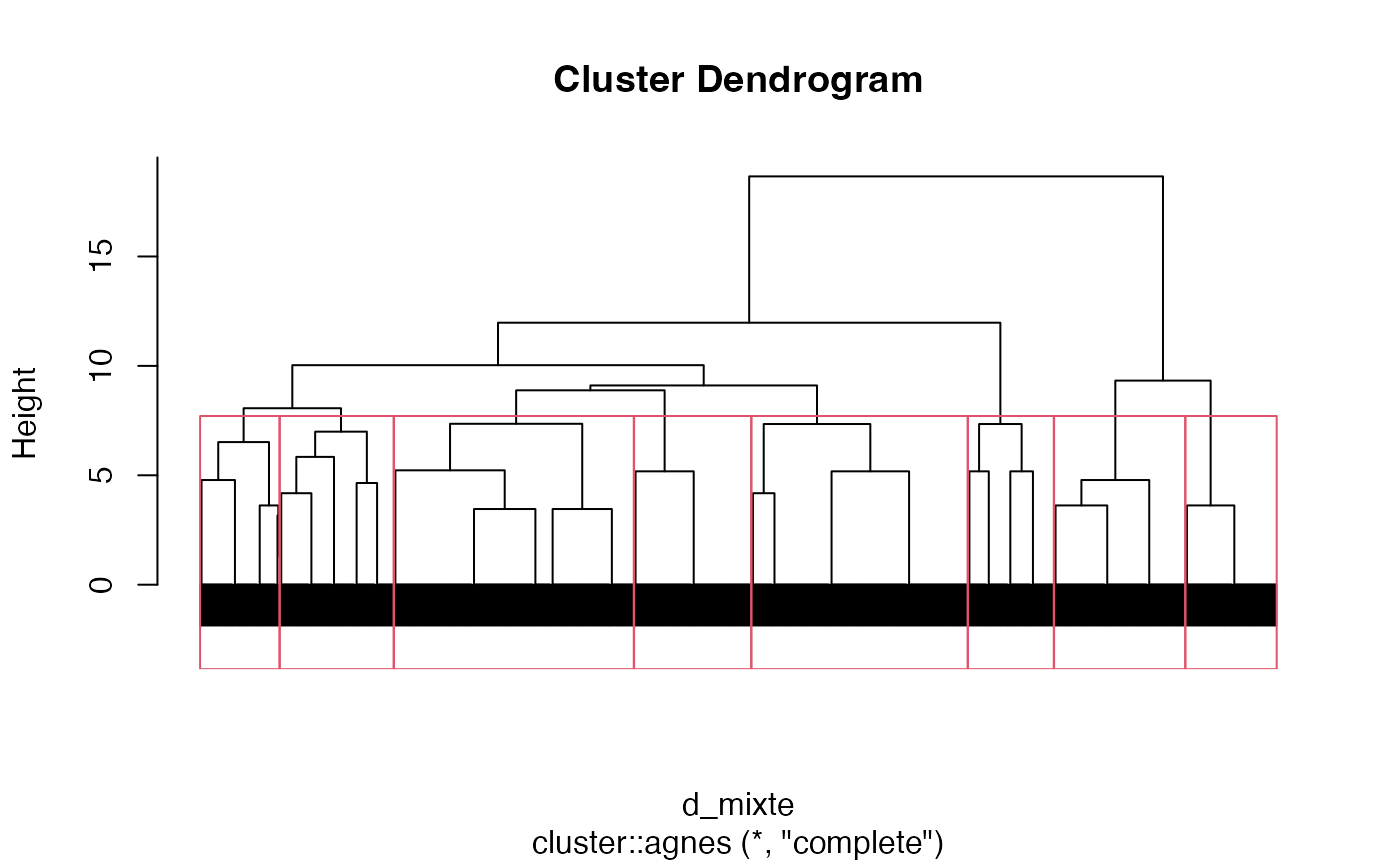

groupes.cah_complete_d_mixte_8 <- cutree(cah.complete,k=8)

Critère Single

arbre2 <- cluster::agnes(d_mixte, method = "single")
cah.single <- as.hclust(arbre2)
plot(cah.single,labels=FALSE)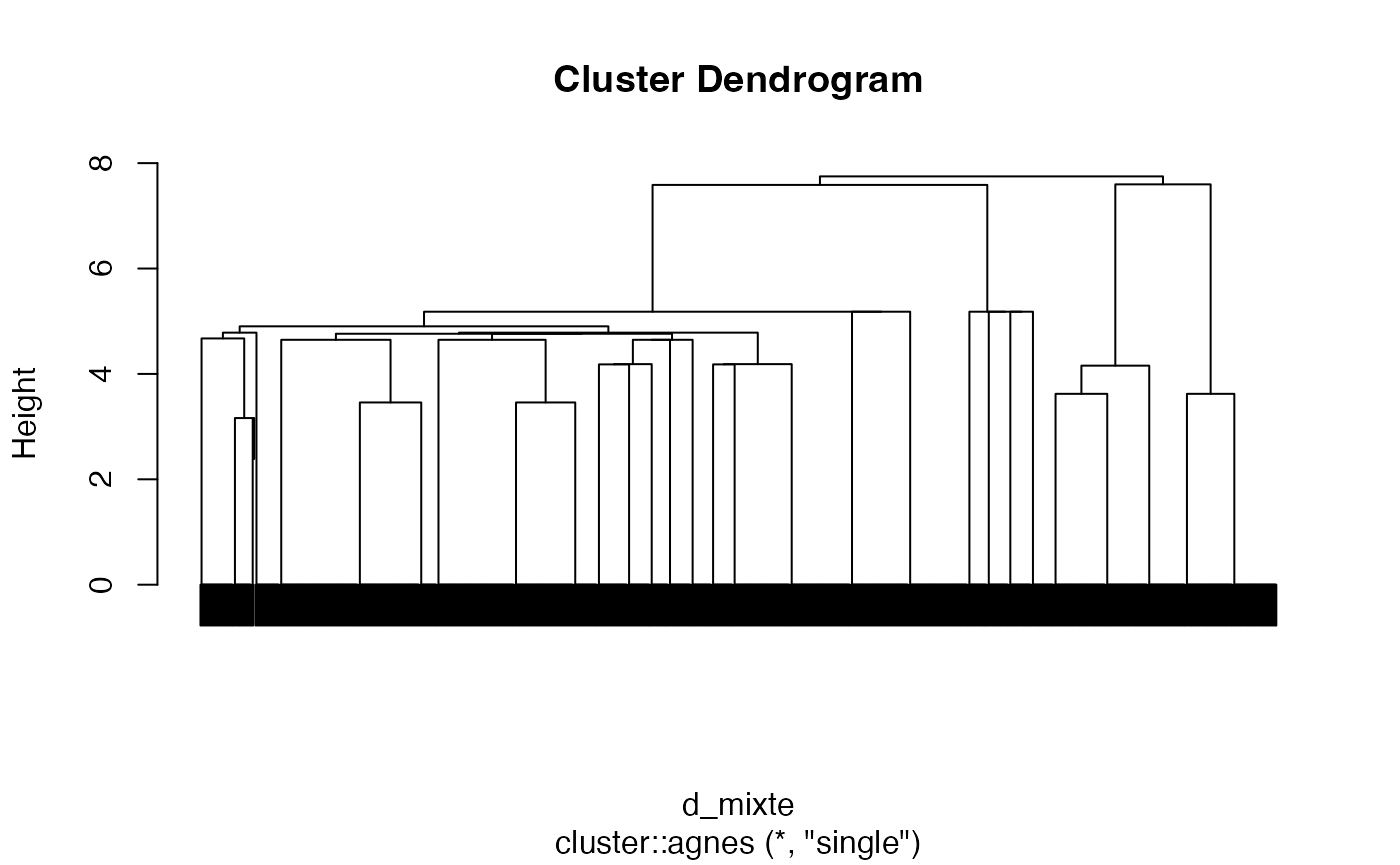

Affiche la décroissance de l’inertie expliquée

inertie <- sort(cah.single$height, decreasing = TRUE)
plot(inertie[1:30], type = "s", xlab = "Nombre de classes", ylab = "Inertie")
points(c(4), inertie[c(4)], col = c("red3"), cex = 2, lwd = 3)

Dendrogramme avec matérialisation des groupes

Découpage en 4 groupes

plot(cah.single,labels=FALSE)
rect.hclust(cah.single,k=4)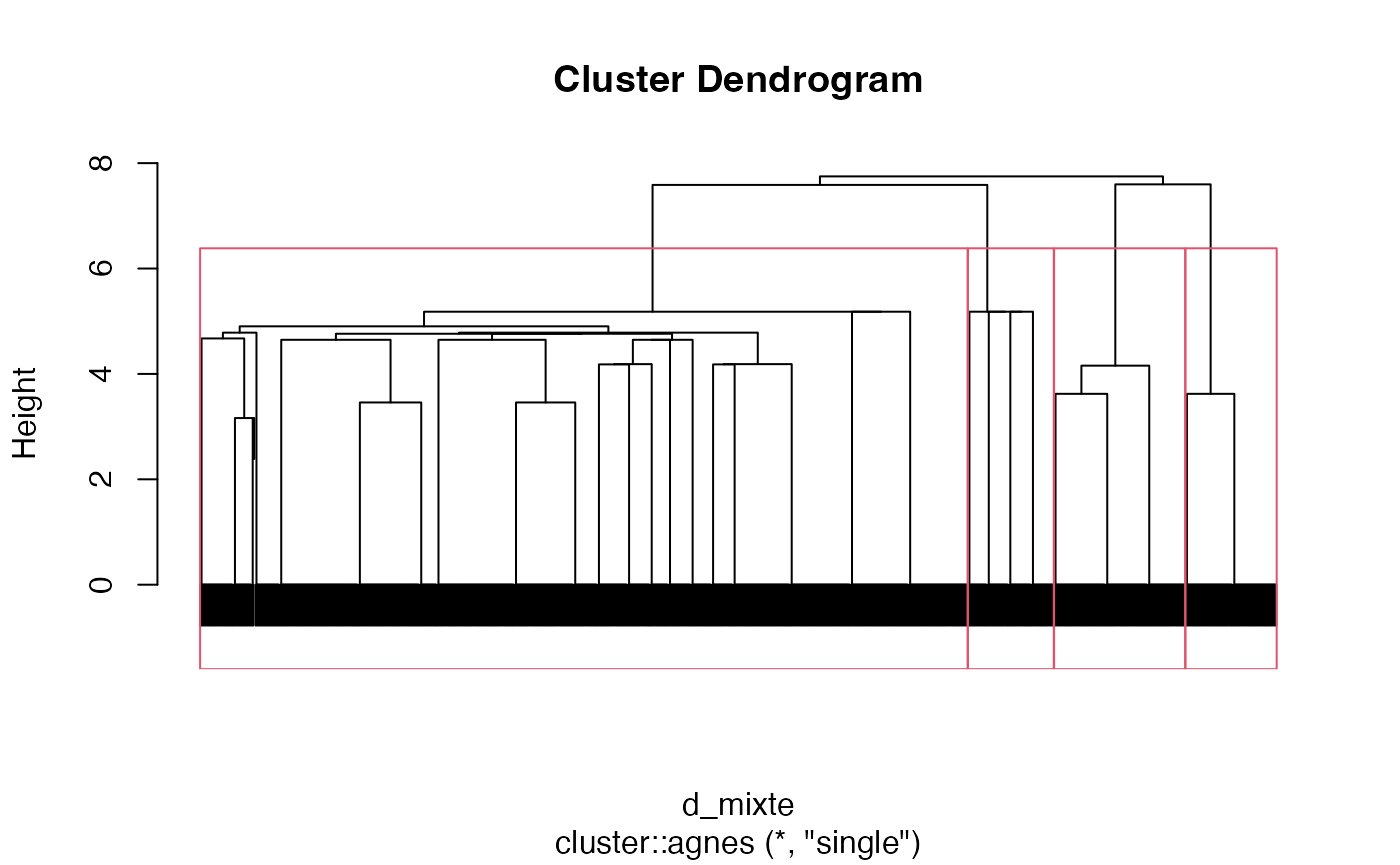

groupes.cah_single_d_mixte_4 <- cutree(cah.single,k=4)

Critère Average

arbre2 <- cluster::agnes(d_mixte, method = "average")
cah.average <- as.hclust(arbre2)
plot(cah.average,labels=FALSE)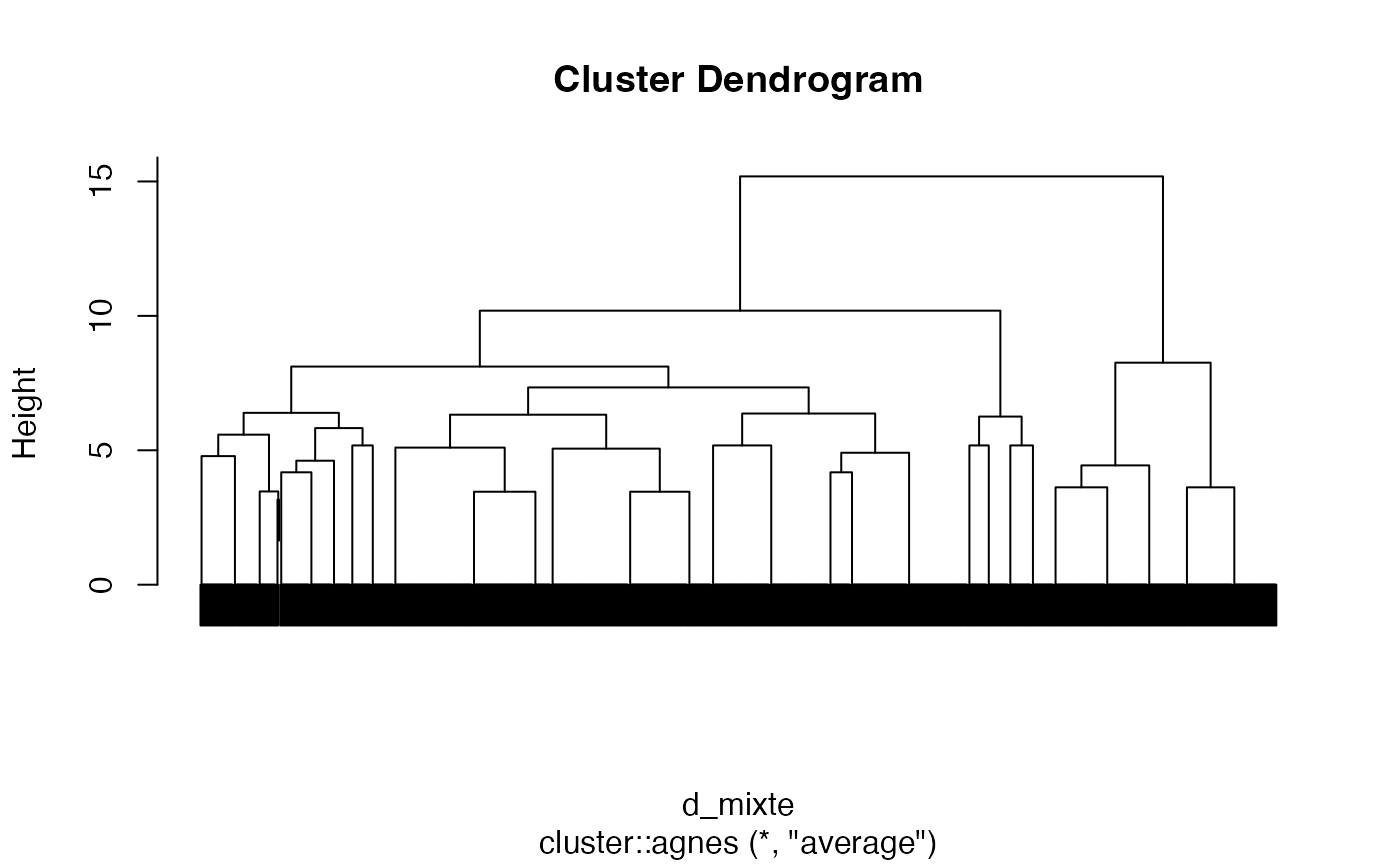

Affiche la décroissance de l’inertie expliquée

inertie <- sort(cah.average$height, decreasing = TRUE)
plot(inertie[1:30], type = "s", xlab = "Nombre de classes", ylab = "Inertie")
points(c(2, 3, 6), inertie[c(2, 3, 6)], col = c("green3", "red3", "blue3"), cex = 2, lwd = 3)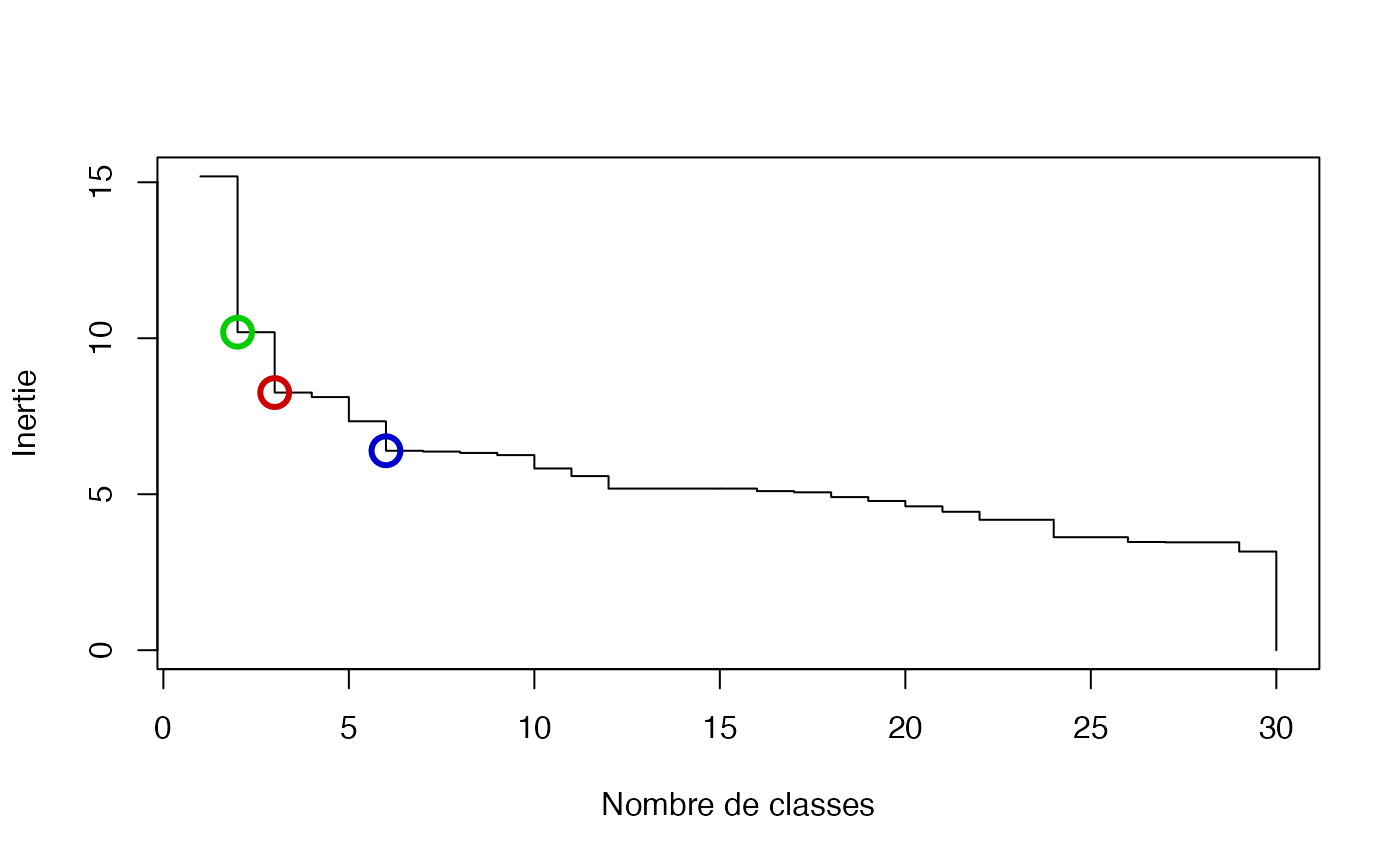

Dendrogramme avec matérialisation des groupes

Découpage en 6 groupes

plot(cah.average,labels=FALSE)
rect.hclust(cah.average,k=6)

groupes.cah_average_d_mixte_6 <- cutree(cah.average,k=6)

Exercice 7.6 : Comparaison des partitions sur la pollution de l’air

Compararaison de partitions (dissim mixte à 8 classes vs distance euclidienne à 8 classes)

Ward PCA vs Ward d_mixte

T_C <- table(groupes.cah_ward_DS,groupes.cah_ward_PCA)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2 # apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2 # apply(T_C,2,sum,na.rm=TRUE)^2
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Exercice 7.7 : K-means sur les données de pollution de l’air

Application des k-means sur plusieurs nombres de classes

groupes.kmeans <- kmeans(air_pol_PCA,centers=2)
inertie_intra <- groupes.kmeans$tot.withinss
R2 <- 1-groupes.kmeans$tot.withinss/groupes.kmeans$totss
for (m in 3:20)
    {groupes.kmeans <- kmeans(air_pol_PCA,centers=m)
     inertie_intra <- groupes.kmeans$tot.withinss
     R2 <- rbind(R2,1-groupes.kmeans$tot.withinss/groupes.kmeans$totss)
    }
m <- 2:20
R2_m <- data.frame(m,R2)
deriv <- matrix(0,nrow=18)
for (i in 1:18)
    {deriv[i]=R2_m[i+1,2]-R2_m[i,2]}
plot(deriv)

Choix du nombre de classes : utilisation du graphique précédent

groupes.kmeans <- kmeans(air_pol_PCA,centers=6)
groupes.kmeans_PCA <- groupes.kmeans$cluster

Comparaisons des résultats avec ceux de l’exercice 7.3

Ward PCA vs K-means PCA

T_C <- table(groupes.kmeans_PCA,groupes.cah_ward_PCA)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Ward d_mixte vs k.means PCA

T_C <- table(groupes.kmeans_PCA,groupes.cah_ward_DS)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Exercice 7.8 : K-means sur les données champignons

Application des k-means sur plusieurs nombres de classes

groupes.kmeans <- kmeans(champ_MCA,centers=2)
inertie_intra <- groupes.kmeans$tot.withinss
R2 <- 1-groupes.kmeans$tot.withinss/groupes.kmeans$totss
for (m in 3:20)
    {groupes.kmeans <- kmeans(champ_MCA,centers=m)
     inertie_intra <- groupes.kmeans$tot.withinss
     R2 <- rbind(R2,1-groupes.kmeans$tot.withinss/groupes.kmeans$totss)
    }
m <- 2:20
R2_m <- data.frame(m,R2)
deriv <- matrix(0,nrow=18)
for (i in 1:18)
    {deriv[i]=R2_m[i+1,2]-R2_m[i,2]}
plot(deriv)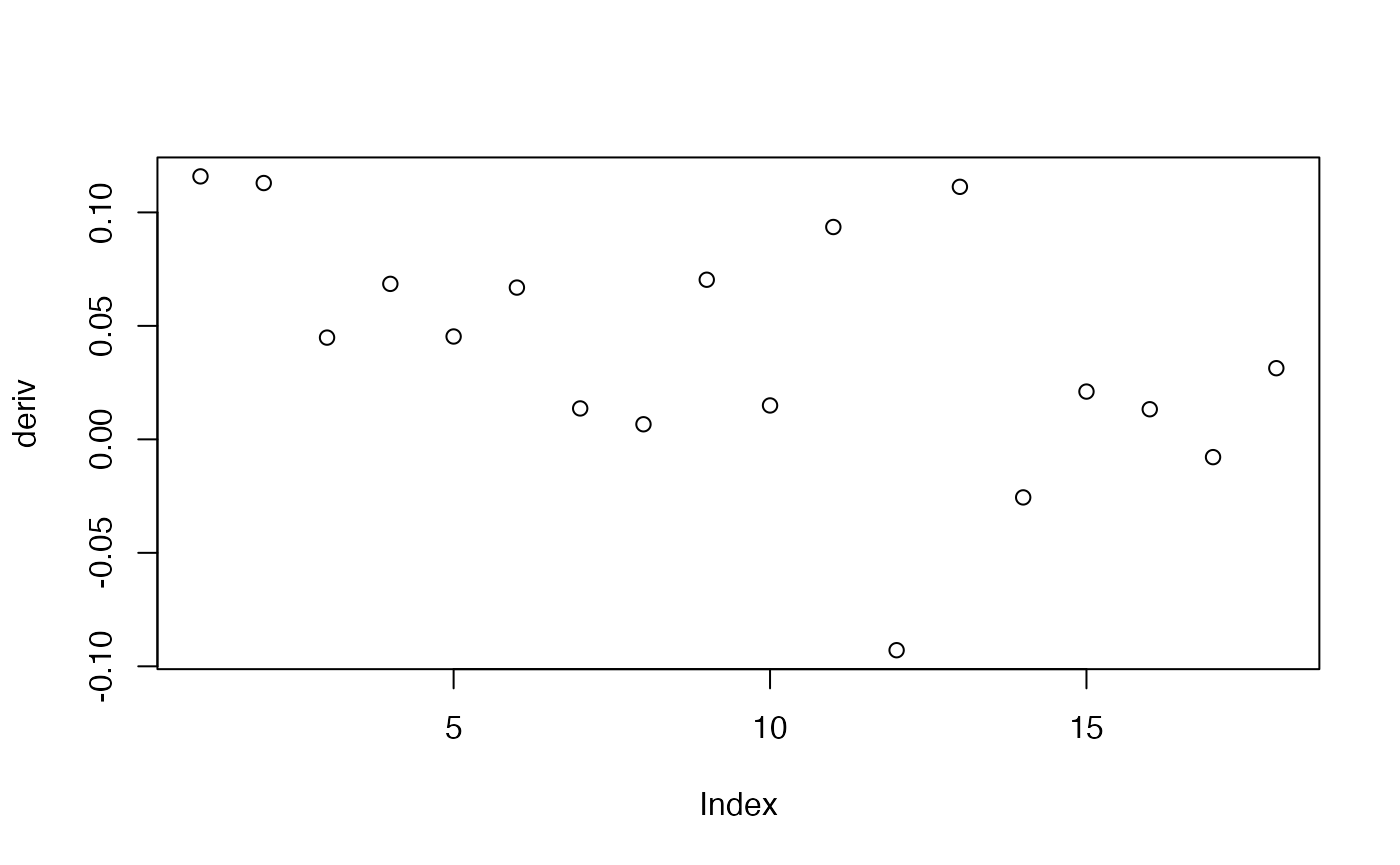

Choix du nombre de classes : utilisation du graphique précédent

groupes.kmeans <- kmeans(champ_MCA,centers=6)
groupes.kmeans_MCA <- groupes.kmeans$cluster

Comparaisons des résultats avec ceux de l’exercice 7.5

Ward MCA vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_ward_d_ACM)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Ward d_mixte_6 vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_ward_d_mixte_6)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Ward d_mixte_8 vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_ward_d_mixte_8)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Complete d_mixte_7 vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_complete_d_mixte_7)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Complete d_mixte_8 vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_complete_d_mixte_8)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Single d_mixte_4 vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_single_d_mixte_4)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Average d_mixte_6 vs K-means MCA

T_C <- table(groupes.kmeans_MCA,groupes.cah_average_d_mixte_6)
nij2 <- T_C^2
ni_2 <- apply(T_C,1,sum,na.rm=TRUE)^2
n_j2 <- apply(T_C,2,sum,na.rm=TRUE)^2
n <- sum(T_C)
n2 <- n^2
a <- sum(nij2)/2
b <- (sum(ni_2)-sum(nij2))/2
c <- (sum(n_j2)-sum(nij2))/2
d <- (n2+sum(nij2)-sum(ni_2)-sum(n_j2))/2
m1 <- a+b
m2 <- a+c
M <- a+b+c+d
Rand <- (a+d)/M
Jaccard <- a/(a+b+c)
Gamma <- (M*a-m1*m2)/sqrt(m1*m2*(M-m1)*(M-m2))

Exercice 7.9 : Interprétation des classes de la typologie

air_pollution_std_cluster <- data.frame(air_pollution_std,groupes.cah_ward_PCA)

library(dplyr)
air_pollution_stat_cluster <- air_pollution_std_cluster %>% group_by(groupes.cah_ward_PCA) %>% summarise(SMIN_moy=mean(SMIN),SMEAN_moy=mean(SMEAN),SMAX_moy=mean(SMAX),PMIN_moy=mean(PMIN),PMEAN_moy=mean(PMEAN),PERWH_moy=mean(PERWH),NONPOOR_moy=mean(NONPOOR),GE65_moy=mean(GE65),LPOP_moy=mean(LPOP),l_pm2_moy=mean(l_pm2),l_pmax_moy=mean(l_pmax),n_m=n()) 
air_pollution_stat_cluster <- data.frame(air_pollution_stat_cluster)

n=50
SMIN_vtest <- (0-air_pollution_stat_cluster$SMIN_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
SMEAN_vtest <- (0-air_pollution_stat_cluster$SMEAN_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
SMAX_vtest <- (0-air_pollution_stat_cluster$SMAX_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
PMIN_vtest <- (0-air_pollution_stat_cluster$PMIN_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
PMEAN_vtest <- (0-air_pollution_stat_cluster$PMEAN)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
PERWH_vtest <- (0-air_pollution_stat_cluster$PERWH_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
NONPOOR_vtest <- (0-air_pollution_stat_cluster$NONPOOR_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
GE65_vtest <- (0-air_pollution_stat_cluster$GE65_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
LPOP_vtest <- (0-air_pollution_stat_cluster$LPOP_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
l_pm2_vtest <- (0-air_pollution_stat_cluster$l_pm2_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
l_pmax_vtest <- (0-air_pollution_stat_cluster$l_pmax_moy)/((n-air_pollution_stat_cluster$n_m)/((n-1)*air_pollution_stat_cluster$n_m))
VTEST_all <- data.frame(SMIN_vtest,SMEAN_vtest,SMAX_vtest,PMIN_vtest,PMEAN_vtest,PERWH_vtest,NONPOOR_vtest,GE65_vtest,LPOP_vtest,l_pm2_vtest,l_pmax_vtest)

VTEST_all <- round(VTEST_all,2)
VTEST_all
#>   SMIN_vtest SMEAN_vtest SMAX_vtest PMIN_vtest PMEAN_vtest PERWH_vtest
#> 1     -17.22      -18.65     -11.42     -12.00       -8.08       -6.16
#> 2       1.35        5.44       5.61       7.33        8.55       14.98
#> 3       8.47        7.24       4.05      -7.52      -12.52       -3.64
#> 4       6.39       10.05       8.04      10.82       12.79       -6.47
#> 5       1.01       -3.40      -5.24      -0.40       -2.46       -0.65
#>   NONPOOR_vtest GE65_vtest LPOP_vtest l_pm2_vtest l_pmax_vtest
#> 1        -15.94     -11.02     -16.76      -20.52        -1.83
#> 2         13.12       9.55       5.24        2.77         7.22
#> 3          7.68       7.59       8.20       12.90       -17.00
#> 4         -6.46      -7.48       2.38        4.74        12.83
#> 5          0.47       0.67       0.62        0.49        -2.96

Tout le code avec R.

Christian Derquenne

2022-09-21

Exercice 7.2 : Construire la matrice de dissimilarités mixtes entre les 1000 champignons

Exercice 7.3 : Application de la classification hiérarchique ascendante de Ward sur les données de pollution de l’air au Etats-Unis

Exercice 7.4 : Application de la classification hiérarchique ascendante de Ward sur les données de caractéristiques des champignons

Exercice 7.5 : Application de la classification hiérarchique à d’autres critères sur les données champignons

Exercice 7.6 : Comparaison des partitions sur la pollution de l’air

Exercice 7.7 : K-means sur les données de pollution de l’air

Exercice 7.8 : K-means sur les données champignons

Exercice 7.9 : Interprétation des classes de la typologie